La logica matematica è il settore della matematica che studia i sistemi formali dal punto di vista del modo di codificare i concetti intuitivi della dimostrazione e di computazione come parte dei fondamenti della matematica. Essa si occupa delle parti della logica che possono essere modellate matematicamente. Altri termini utilizzati spesso nel passato sono logica simbolica (termine contrapposto a logica filosofica) e metamatematica, termine che ora si applica più specificamente a taluni aspetti della teoria della dimostrazione.

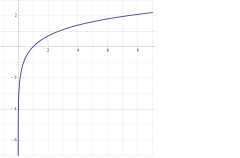
Il logaritmo naturale (o logaritmo neperiano) è il logaritmo in base e, dove e {\displaystyle e} è uguale a 2,718 28 … {\displaystyle 2{,}71828\ldots } Il logaritmo naturale è definito per tutte le x {\displaystyle x} reali e positive, ma anche per i numeri complessi diversi da zero.

In trigonometria l'arcotangente è definita come funzione inversa della restrizione della funzione tangente all'intervallo ( − π 2 , π 2 ) ⊂ R . {\displaystyle \left(-{\pi \over 2},{\pi \over 2}\right)\subset \mathbb {R} .} Il nome può esser fatto derivare dalla locuzione uno degli archi la cui tangente è la misura dell'angolo (infatti i radianti, unità di misurazione della funzione arcotangente, corrispondono al rapporto tra la lunghezza dell'arco di circonferenza individuato da un dato angolo e il raggio della circonferenza stessa). Con maggior precisione, si potrebbe affermare che l'arcotangente di x {\displaystyle x} è l'angolo di valore assoluto minore la cui tangente è x {\displaystyle x} . È necessario considerare la restrizione della funzione tangente all'intervallo precedentemente indicato in modo da preservare l'invertibilità della funzione.

In matematica, in particolare in trigonometria, l'arcocoseno è definito come funzione inversa del coseno di un angolo. La funzione coseno non è biiettiva, quindi non invertibile. È possibile, però, applicare un restringimento del dominio e del codominio in modo da renderla sia iniettiva che suriettiva. Per convenzione si preferisce restringere il dominio della funzione coseno nell'intervallo [ 0 , π ] {\displaystyle \left[0,\pi \right]} .