Il teorema di Perron-Frobenius afferma che, se A {\displaystyle A} è una matrice non negativa (cioè, con tutti gli elementi maggiori o uguali a zero) primitiva e irriducibile allora L'autovalore di modulo massimo λ {\displaystyle \lambda } di A {\displaystyle A} è reale positivo Esso è un autovalore semplice L'autovettore corrispondente ha tutte le componenti positive L'autovettore corrispondente è l'unico autovettore non negativo di A {\displaystyle A} L'autovalore di modulo massimo, visto come funzione ρ ( A ) {\displaystyle \rho (A)} della matrice A {\displaystyle A} , è una funzione strettamente crescente in ognuno dei suoi elementi: cioè, se B ≥ A {\displaystyle B\geq A} (s'intende che tale disuguaglianza valga elemento per elemento) e B ≠ A {\displaystyle B\neq A} , allora ρ ( B ) > ρ ( A ) {\displaystyle \rho (B)>\rho (A)} Il teorema di Perron-Frobenius è un risultato abbastanza potente ma elementare di algebra lineare che solitamente non si vede nei primi corsi. Una sua applicazione è per esempio quella di assicurare l'esistenza di misure invarianti per catene di Markov finite.

In matematica, una norma matriciale è la naturale estensione alle matrici del concetto di norma definito per i vettori.

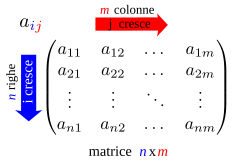
In matematica, in particolare in algebra lineare, una matrice è una tabella ordinata di elementi. Ad esempio: ( 1 0 5 1 − 2 0 ) {\displaystyle {\begin{pmatrix}1&0&5\\1&-2&0\end{pmatrix}}} Le matrici sono ampiamente usate in matematica e in tutte le scienze per la loro capacità di rappresentare in maniera utile e concisa diversi oggetti matematici, come valori che dipendono da due parametri o anche sistemi lineari, cosa, quest'ultima, che le rende uno strumento centrale dell'analisi matematica.