biblio toscana

Una funzione di variabile reale è una funzione nel senso più comune del termine, cioè una legge che agisce sui numeri (reali) e li trasforma in altri numeri reali. Più precisamente, una tale funzione si presenta come definita sul dominio R {\displaystyle \mathbb {R} } o un suo sottoinsieme e a valori sempre reali. Se consideriamo invece come dominio il prodotto cartesiano di R {\displaystyle \mathbb {R} } due, tre, n {\displaystyle n} volte, otteniamo una funzione (ad esempio la funzione che calcola la somma di due numeri, o il loro prodotto) che prende come argomento non uno solo, ma due, tre, n {\displaystyle n} numeri reali e li trasforma in un unico numero reale. Si dice dunque che l'argomento della funzione è una n {\displaystyle n} -upla di numeri reali, o un vettore di R n {\displaystyle \mathbb {R} ^{n}} . Si può ulteriormente separare il discorso, considerando adesso funzioni che hanno come output non uno, bensì più numeri reali: la funzione che dati due interi restituisce il loro quoziente e resto ha due argomenti e due uscite, cioè un vettore di R 2 {\displaystyle \mathbb {R} ^{2}} . Si parlerà dunque di funzioni scalari se il codominio è un sottoinsieme di R {\displaystyle \mathbb {R} } , di funzioni vettoriali se il codominio è un sottoinsieme di R n {\displaystyle \mathbb {R} ^{n}} per un certo n > 1 {\displaystyle n>1} . In particolare, si dirà campo vettoriale una funzione da (un sottoinsieme di) R n {\displaystyle \mathbb {R} ^{n}} (con n > 1 {\displaystyle n>1} ) in R n {\displaystyle \mathbb {R} ^{n}} stesso. In generale abbiamo dunque quattro situazioni possibili (considerando n , m > 1 {\displaystyle n,m>1} ): f : R → R {\displaystyle f\colon \mathbb {R} \to \mathbb {R} } : la situazione più classica; f : R n → R {\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} } : una funzione scalare in n {\displaystyle n} variabili; f : R → R n {\displaystyle f\colon \mathbb {R} \to \mathbb {R} ^{n}} : una funzione vettoriale di una variabile (ad esempio quella che dato un numero restituisce parte intera e parte frazionaria); f : R n → R m {\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} : una funzione vettoriale in n {\displaystyle n} variabili.Le funzioni (scalari) di una variabile reale si classificano in: funzioni algebriche; funzioni trascendenti.

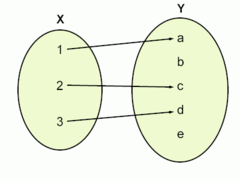
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).