biblio toscana

Come riforma Gelmini si indica comunemente l'insieme degli atti normativi della Repubblica Italiana – emanati durante il governo Berlusconi III – durante la permanenza in carica del Ministro dell'istruzione, dell'università e della ricerca Mariastella Gelmini, riguardanti il settore dell'istruzione in Italia. Emanati tra il 2008 ed il 2010, modificarono profondamente la riforma Moratti del 2003.

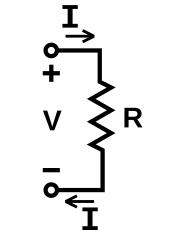
La legge di Ohm è una legge empirica che descrive accuratamente la conduttività della maggior parte dei materiali conduttori al variare della corrente per molti ordini di grandezza, stabilendo che la differenza di potenziale tra due punti di un conduttore è direttamente proporzionale alla corrente che scorre tra di essi, a mezzo di una costante di proporzionalità che è detta resistenza elettrica. Vi sono alcuni materiali che non obbediscono a tale legge e vengono chiamati "non-ohmici". Il nome è dovuto al fisico tedesco Georg Ohm, che, in un trattato pubblicato nel 1827, descrisse la misura della corrente e della differenza di potenziale attraverso dei semplici circuiti con fili di diversa lunghezza, anche se la formulazione originale è più complessa della forma attuale.

La legge dei grandi numeri oppure teorema di Bernoulli (in quanto la sua prima formulazione è dovuta a Jakob Bernoulli), descrive il comportamento della media di una sequenza di n {\displaystyle n} prove di una variabile casuale, indipendenti e caratterizzate dalla stessa distribuzione di probabilità (n misure della stessa grandezza, n {\displaystyle n} lanci della stessa moneta, ecc.), al tendere ad infinito della numerosità della sequenza stessa ( n {\displaystyle n} ). In altre parole, grazie alla legge dei grandi numeri, possiamo fidarci che la media sperimentale, che calcoliamo a partire da un numero sufficiente di campioni, sia sufficientemente vicina alla media vera, ovvero quella calcolabile teoricamente. Che cosa significhi "ragionevolmente sicuri" dipende da quanto vogliamo essere precisi nel nostro test: con dieci prove, avremmo una stima grossolana, con cento, ne otterremmo una molto più precisa, con mille, ancora di più, e così via: il valore di n {\displaystyle n} che siamo disposti ad accettare come sufficiente dipende dal grado di casualità che riteniamo necessario per il dato in questione. In termini generici, per la legge dei grandi numeri si può dire: che la media della sequenza è un'approssimazione, che migliora al crescere di n , {\displaystyle n,} della media della distribuzione; e che, viceversa, si può prevedere che sequenze siffatte mostreranno una media tanto più spesso e tanto più precisamente prossima alla media della distribuzione quanto più grande sarà n {\displaystyle n} .Un caso particolare di applicazione della legge dei grandi numeri è la previsione probabilistica della proporzione di successi in una successione di n {\displaystyle n} realizzazioni indipendenti di un evento E , {\displaystyle E,} ossia la frequenza di E {\displaystyle E} nelle n {\displaystyle n} misurazioni: per n {\displaystyle n} che tende a infinito, la proporzione di successi converge alla probabilità di E . {\displaystyle E.}