biblio toscana

Le leggi di Keplero sono tre leggi concernenti il movimento dei pianeti. Sono il principale contributo di Johannes von Kepler all'astronomia e alla meccanica. L'astronomo tedesco le derivò studiando le osservazioni di Tycho Brahe. Isaac Newton, successivamente, dedusse dalle leggi di Keplero la spiegazione dinamica dei moti planetari introducendo, quale causa del moto, una forza, detta forza di gravitazione universale. Newton dimostrò anche il teorema inverso, ossia che dalla sua legge generale del moto e dalla forza di gravità si ottengono, nella stessa maniera, le leggi di Keplero.

La legge delle proporzioni definite, è una legge ponderale, enunciata da Joseph Louis Proust nel 1798, è una legge che regola la formazione dei composti chimici a partire dagli elementi che li compongono. Essa recita: quando due o più elementi reagiscono per formare un determinato composto, si combinano sempre secondo proporzioni in massa definite e costanti.Ad esempio il carbonato di rame, qualunque fosse la sua origine (naturale o preparato in laboratorio), conteneva rame, carbonio e ossigeno sempre nelle stesse proporzioni. Secondo Proust, "...un composto è un prodotto privilegiato al quale la natura ha dato una composizione costante" (Composto stechiometrico). Esistono però delle eccezioni costituite dai cosiddetti composti non stechiometrici.

In chimica la legge della conservazione della massa o legge di Lavoisier è una legge ponderale ed enuncia che: in una reazione chimica, la somma delle masse dei reagenti è uguale alla somma delle masse dei prodotti.

La legge Rosato, dal nome del suo relatore Ettore Rosato, ufficialmente legge 3 novembre 2017, n. 165 e comunemente nota come Rosatellum bis o semplicemente Rosatellum, è una legge elettorale della Repubblica Italiana che disciplina l'elezione della Camera dei deputati e del Senato della Repubblica. È stata approvata in via definitiva al Senato il 26 ottobre 2017 e sostituisce la precedente legge elettorale italiana del 2015, nota come Italicum (valida solo per la Camera dei deputati) e la previgente legge Calderoli (in vigore per il Senato della Repubblica, non abrogata dall'Italicum), ambedue soggette a pronunce di parziale incostituzionalità da parte della Corte costituzionale. Ha visto la sua prima applicazione alle elezioni politiche del 4 marzo 2018.

Come riforma Gelmini si indica comunemente l'insieme degli atti normativi della Repubblica Italiana – emanati durante il governo Berlusconi III – durante la permanenza in carica del Ministro dell'istruzione, dell'università e della ricerca Mariastella Gelmini, riguardanti il settore dell'istruzione in Italia. Emanati tra il 2008 ed il 2010, modificarono profondamente la riforma Moratti del 2003.

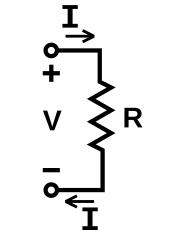
La legge di Ohm è una legge empirica che descrive accuratamente la conduttività della maggior parte dei materiali conduttori al variare della corrente per molti ordini di grandezza, stabilendo che la differenza di potenziale tra due punti di un conduttore è direttamente proporzionale alla corrente che scorre tra di essi, a mezzo di una costante di proporzionalità che è detta resistenza elettrica. Vi sono alcuni materiali che non obbediscono a tale legge e vengono chiamati "non-ohmici". Il nome è dovuto al fisico tedesco Georg Ohm, che, in un trattato pubblicato nel 1827, descrisse la misura della corrente e della differenza di potenziale attraverso dei semplici circuiti con fili di diversa lunghezza, anche se la formulazione originale è più complessa della forma attuale.

La Legge di Murphy è un insieme di paradossi pseudoscientifici a carattere ironico e caricaturale. Si possono idealmente riassumere nel primo assioma, che è in realtà la "Legge di Murphy" vera e propria, che ha dato il titolo a tutto il pensiero "murphologico": L'autore e stilatore della “summa” sulla "murphologia" è Arthur Bloch. Si tratta di un compendio di frasi umoristiche il cui intento è essenzialmente quello di deridere ogni negatività che il quotidiano propone. Il meccanismo è ogni volta lo stesso: immagini e scenette frustranti, nelle quali è facile per molti ritrovarsi, vengono descritte da Bloch con frasi didascaliche, confezionate spesso e volentieri in forma statistico-matematica, così da liberare il vissuto dal contingente, dal personale e donargli un rilievo di "validità universale", nei fatti tuttavia inesistente. Negli Stati Uniti la legge di Murphy è talmente famosa da trovare posto nel Funk and Wagnalls Standard College Dictionary.

Cerere (dal latino Cerēs, Cerere, in origine chiamato Cerere Ferdinandea, catalogato come 1 Ceres secondo la designazione asteroidale) è l'asteroide più massiccio della fascia principale del sistema solare; la sua scoperta, avvenuta il 1º gennaio 1801 a opera di Giuseppe Piazzi dall'osservatorio astronomico di Palermo, è stata la prima per un asteroide e per mezzo secolo Cerere è stato considerato l'ottavo pianeta. Dal 2006 Cerere è l'unico asteroide del sistema solare interno considerato un pianeta nano, alla stregua di Plutone, Makemake, Haumea ed Eris, che però appartengono tutti al sistema solare esterno.Il suo diametro varia dai 900 ai 1000 km e la sua massa è pari al 32% di quella dell'intera fascia principale. La fascia di Edgeworth-Kuiper contiene oggetti molto più grandi di Cerere; oltre ai pianeti nani già citati, si ricordano Quaoar, Orco e Sedna. Le osservazioni astronomiche hanno rivelato che ha forma sferica. La sua superficie è probabilmente composta da un miscuglio di ghiaccio d'acqua e vari minerali, come carbonati e argille idrate. Cerere ha subito un processo di differenziazione, che ha condotto alla formazione di un nucleo roccioso e di un mantello di materiali ghiacciati, e potrebbe ospitare un oceano di acqua liquida sotto la superficie.Dalla Terra appare come un oggetto stellare la cui magnitudine varia tra 6,7 e 9,3. La sua luminosità è troppo debole perché possa essere visto a occhio nudo. Il 27 settembre 2007 la NASA ha lanciato la missione Dawn che ha visitato Vesta nel biennio 2011–2012; la sonda Dawn è entrata in orbita attorno a Cerere il 6 marzo 2015..