Il teorema di Abel-Ruffini afferma che non esiste una relazione risolutiva generale esprimibile tramite radicali per le equazioni polinomiali di grado 5 o superiore. Il teorema fu provato per la prima volta da Paolo Ruffini nel 1799, ma la sua dimostrazione fu generalmente ignorata. Sebbene contenesse una piccola lacuna, fu piuttosto innovativa nell'uso dei gruppi di permutazione. Il teorema è anche attribuito a Niels Henrik Abel, che pubblicò una dimostrazione nel 1824.
La storia della matematica ha origine con il concetto di numero e con le prime scoperte matematiche, proseguendo attraverso l'evoluzione nel corso dei secoli dei propri metodi e delle notazioni matematiche il cui uso si sussegue nel tempo. Un aspetto importante della matematica consiste nel fatto che essa si è sviluppata indipendentemente in culture completamente differenti arrivando in molti casi agli stessi risultati: spesso un contatto o una reciproca influenza tra popoli differenti ha portato all'introduzione di nuove idee e a un avanzamento delle conoscenze matematiche, a volte si è visto invece un regredire improvviso della cultura matematica presso alcuni popoli; la matematica moderna ha invece potuto avvalersi dei contributi di persone di tutti i paesi. L'attività svolta dai matematici moderni è molto diversa da quella dei primi matematici delle civiltà antiche; inizialmente la matematica si basò sul concetto di numero, concetto sviluppatosi nella preistoria. La matematica è stata infatti una tra le prime discipline a svilupparsi: evidenze archeologiche mostrano la conoscenza rudimentale di alcune nozioni matematiche molto prima dell'invenzione della scrittura.
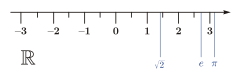
In matematica, i numeri reali possono essere descritti in maniera non formale come numeri ai quali è possibile attribuire uno sviluppo decimale finito o infinito, come π = 3 , 141592 … {\displaystyle \pi =3,141592\ldots } I numeri reali possono essere positivi, negativi o nulli e comprendono, come casi particolari, i numeri interi (come 12 {\displaystyle 12} ), i numeri razionali (come − 22 / 7 {\displaystyle -22/7} ) e i numeri irrazionali algebrici (come 2 {\displaystyle {\sqrt {2}}} ) e trascendenti (come π {\displaystyle \pi } ed e {\displaystyle e} ). Un numero reale razionale presenta uno sviluppo decimale finito o periodico; ad esempio 1 / 3 = 0 , 333333 … {\displaystyle 1/3=0,333333\ldots } è razionale. L'insieme dei numeri reali è generalmente indicato con la lettera R o R {\displaystyle \mathbb {R} } . I numeri reali possono essere messi in corrispondenza biunivoca con i punti di una retta, detta retta numerica o retta reale. La definizione formale dei numeri reali ha rappresentato uno degli sviluppi più significativi del XIX secolo. Tra le definizioni maggiormente adottate oggi figurano le classi di equivalenza di successioni di Cauchy di numeri razionali, le sezioni di Dedekind, una ridefinizione del termine "rappresentazione decimale" e una definizione assiomatica come unico campo archimedeo completo ordinato. I termini reale e immaginario sono stati introdotti ne La Géometrie di René Descartes (1637), relativamente allo studio delle radici delle equazioni. Per estensione diversi autori hanno cominciato a parlare di numeri reali e numeri immaginari. Nel 1874 appare un articolo fondamentale di Georg Cantor nel quale l'autore prende in considerazione l'insieme dei numeri reali dimostrando che tale insieme non è numerabile.
