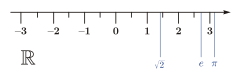
In matematica, i numeri reali possono essere descritti in maniera non formale come numeri ai quali è possibile attribuire uno sviluppo decimale finito o infinito, come π = 3 , 141592 … {\displaystyle \pi =3,141592\ldots } I numeri reali possono essere positivi, negativi o nulli e comprendono, come casi particolari, i numeri interi (come 12 {\displaystyle 12} ), i numeri razionali (come − 22 / 7 {\displaystyle -22/7} ) e i numeri irrazionali algebrici (come 2 {\displaystyle {\sqrt {2}}} ) e trascendenti (come π {\displaystyle \pi } ed e {\displaystyle e} ). Un numero reale razionale presenta uno sviluppo decimale finito o periodico; ad esempio 1 / 3 = 0 , 333333 … {\displaystyle 1/3=0,333333\ldots } è razionale. L'insieme dei numeri reali è generalmente indicato con la lettera R o R {\displaystyle \mathbb {R} } . I numeri reali possono essere messi in corrispondenza biunivoca con i punti di una retta, detta retta numerica o retta reale. La definizione formale dei numeri reali ha rappresentato uno degli sviluppi più significativi del XIX secolo. Tra le definizioni maggiormente adottate oggi figurano le classi di equivalenza di successioni di Cauchy di numeri razionali, le sezioni di Dedekind, una ridefinizione del termine "rappresentazione decimale" e una definizione assiomatica come unico campo archimedeo completo ordinato. I termini reale e immaginario sono stati introdotti ne La Géometrie di René Descartes (1637), relativamente allo studio delle radici delle equazioni. Per estensione diversi autori hanno cominciato a parlare di numeri reali e numeri immaginari. Nel 1874 appare un articolo fondamentale di Georg Cantor nel quale l'autore prende in considerazione l'insieme dei numeri reali dimostrando che tale insieme non è numerabile.
In matematica, un numero primo (in breve anche primo) un numero intero positivo che abbia esattamente due divisori distinti. In modo equivalente si pu definire come un numero naturale maggiore di 1 che sia divisibile solamente per 1 e per s stesso; al contrario, un numero maggiore di 1 che abbia pi di due divisori detto composto. Ad esempio 2, 3 e 5 sono primi mentre 4 e 6 non lo sono perch sono divisibili rispettivamente anche per 2 e per 2 e 3. L'unico numero primo pari 2, in quanto tutti gli altri numeri pari sono divisibili per 2. La successione dei numeri primi comincia con 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 Quello di numero primo uno dei concetti basilari della teoria dei numeri, la parte della matematica che studia i numeri interi: l'importanza sta nella possibilit di costruire con essi, attraverso la moltiplicazione, tutti gli altri numeri interi, nonch l'unicit di tale fattorizzazione. I primi sono inoltre infiniti e la loro distribuzione tuttora oggetto di molte ricerche. I numeri primi sono oggetto di studio fin dall'antichit : i primi risultati risalgono infatti agli antichi Greci, e in particolare agli Elementi di Euclide, scritti attorno al 300 a.C. Ciononostante, numerose congetture che li riguardano non sono state ancora dimostrate; tra le pi note vi sono l'ipotesi di Riemann, la congettura di Goldbach e quella dei primi gemelli, indimostrate a pi di un secolo dalla loro formulazione. Essi sono rilevanti anche in molti altri ambiti della matematica pura, come ad esempio l'algebra o la geometria; recentemente hanno assunto un'importanza cruciale anche nella matematica applicata, e in particolare nella crittografia.
In matematica i numeri naturali sono quei numeri usati per contare e ordinare. Nel linguaggio comune i "numeri cardinali" sono quelli usati per contare e i "numeri ordinali" sono quelli usati per ordinare. I numeri naturali corrispondono all'insieme {0, 1, 2, 3, 4, …}. Essi vengono fatti corrispondere biunivocamente all'insieme dei numeri interi non negativi {0, +1, +2, +3, +4, …}. Talvolta vengono usati anche per indicare l'insieme dei numeri interi positivi {1, 2, 3, 4, …}.
In matematica, un numero è un modo di esprimere una quantità, oppure la posizione in un elenco di elementi, oppure il rapporto tra grandezze dello stesso tipo. Il concetto di numero nasce per la necessità del conteggio, come astrazione del concetto di quantità, realizzato attraverso una corrispondenza biunivoca tra elementi di due insiemi distinti. Si definisce operazione numerica una procedura che, a partire da uno o più numeri, genera un altro numero. Le operazioni numeriche fondamentali (dette anche "operazioni aritmetiche") sono: l'addizione, la sottrazione, la moltiplicazione e la divisione. Lo studio delle proprietà di queste operazioni è parte dell'algebra elementare. Un insieme di numeri è frequentemente espresso attraverso il concetto di campo.
