biblio toscana

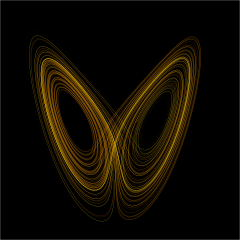
In matematica la teoria del caos è lo studio, attraverso modelli propri della fisica matematica, dei sistemi dinamici che esibiscono una sensibilità esponenziale rispetto alle condizioni iniziali. I sistemi di questo tipo, pur governati da leggi deterministiche, sono in grado di esibire un'empirica casualità nell'evoluzione delle variabili dinamiche. Questo comportamento casuale è solo apparente, dato che si manifesta nel momento in cui si confronta l'andamento temporale asintotico di due sistemi con configurazioni iniziali arbitrariamente simili tra loro.

La topologia (dal greco τόπος, tópos, "luogo", e λόγος, lógos, "studio", col significato quindi di "studio dei luoghi'") è una branca della geometria che studia le proprietà delle figure, e in generale degli oggetti matematici, che non cambiano quando viene effettuata una deformazione senza "strappi", "sovrapposizioni" o "incollature". È una delle più importanti branche della matematica moderna. Concetti fondamentali come convergenza, limite, continuità, connessione o compattezza trovano nella topologia la loro migliore formalizzazione. Si basa essenzialmente sui concetti di spazio topologico, funzione continua e omeomorfismo. Col termine topologia si indica anche la collezione di aperti che definisce uno spazio topologico. Per esempio un cubo e una sfera sono oggetti topologicamente equivalenti (cioè omeomorfi), perché possono essere deformati l'uno nell'altro senza ricorrere ad alcuna incollatura, strappo o sovrapposizione; una sfera e un toro invece non lo sono, perché il toro contiene un "buco" che non può essere eliminato da una deformazione.