biblio toscana

Il testo argomentativo è un tipo di testo che ha come obiettivo principale dare sostentamento alla o alle tesi formulate dall'autore. La forza delle tesi è illustrata mediante l'esposizione coerente e logica di argomentazioni o ragioni, che hanno come proposito persuadere o convincere il lettore in relazione ad un punto di vista determinato e adeguatamente elaborato. L'argomentazione si riferisce all'esposizione di una serie di ragioni per dimostrare o giustificare qualcosa. Di conseguenza, l'argomentazione di solito non è data nella sua forma pura e di solito è combinata con l'esposizione. Mentre l'esposizione si limita a mostrare, l'argomentazione cerca di dimostrare, convincere o cambiare le idee. Pertanto, in un testo argomentativo, oltre alla funzione appellativa presente nello sviluppo degli argomenti, la funzione rappresentativa appare nella parte in cui la tesi è esposta. Una vasta gamma di testi, soprattutto scientifici, filosofici, saggi letterari, produzioni politiche e giudiziarie, testi di opinione giornalistica e alcuni messaggi pubblicitari, possono essere considerati testi argomentativi. Nel linguaggio orale, oltre ad apparire frequentemente nelle conversazioni quotidiane (anche se non molto spesso), è la forma dominante nei dibattiti, nei colloqui o nelle tavole rotonde. I testi argomentativi sono quelli in cui l'intenzione comunicativa principale dello scrittore è quella di offrire la visione soggettiva dell'autore su un certo argomento. L'argomentazione è, per definizione, una procedura persuasiva. A parte tutte le informazioni che possono essere fornite attraverso questi testi (il che implica che c'è quasi sempre anche l'esposizione), c'è implicitamente l'intenzione di convincere il destinatario di ciò che viene esposto.

In matematica, una relazione binaria R in un insieme X è simmetrica se e solo se, presi due elementi qualsiasi a e b, vale che se a è in relazione con b allora anche b è in relazione con a. In simboli: ∀ a , b ∈ X , a R b ⇒ b R a {\displaystyle \forall a,b\in X,\ aRb\Rightarrow bRa} Ad esempio, "è sposato/a con" è una relazione simmetrica, mentre "è figlio di" non lo è. Una relazione di simmetria che è anche transitiva e riflessiva è una relazione di equivalenza.

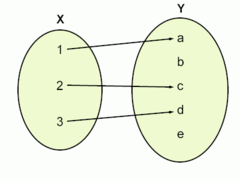
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).