biblio toscana

La distribuzione normale (o distribuzione di Gauss dal nome del matematico tedesco Carl Friedrich Gauss), nella teoria della probabilità, è una distribuzione di probabilità continua che è spesso usata come prima approssimazione per descrivere variabili casuali a valori reali che tendono a concentrarsi attorno a un singolo valor medio. Il grafico della funzione di densità di probabilità associata è simmetrico e ha una forma a campana, nota come campana di Gauss (o anche come curva degli errori, curva a campana, ogiva).

Nella teoria delle probabilità la distribuzione χ 2 {\displaystyle \chi ^{2}} (chi quadrato o chi-quadro) è la distribuzione di probabilità della somma dei quadrati di variabili aleatorie normali indipendenti. In statistica viene particolarmente utilizzata per l'omonimo test di verifica d'ipotesi (test χ2).

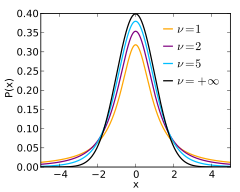
Nella teoria delle probabilità la distribuzione di Student, o t di Student, è una distribuzione di probabilità continua che governa il rapporto tra due variabili aleatorie, la prima con distribuzione normale e la seconda, al quadrato, segue una distribuzione chi quadrato. Questa distribuzione interviene nella stima della media di una popolazione che segue la distribuzione normale, e viene utilizzata negli omonimi test t di Student per la significatività e per ogni intervallo di confidenza della differenza tra due medie.

In teoria delle probabilità la distribuzione di Poisson (o poissoniana) è una distribuzione di probabilità discreta che esprime le probabilità per il numero di eventi che si verificano successivamente ed indipendentemente in un dato intervallo di tempo, sapendo che mediamente se ne verifica un numero λ {\displaystyle \lambda } . Ad esempio, si utilizza una distribuzione di Poisson per misurare il numero di chiamate ricevute in un call-center in un determinato arco temporale, come una mattinata lavorativa. Questa distribuzione è anche nota come legge degli eventi rari. Prende il nome dal matematico francese Siméon-Denis Poisson.

La distribuzione cinematografica è una fase del processo di diffusione e presentazione al pubblico di un film. Della distribuzione cinematografica si occupa spesso una compagnia indipendente, una società controllata o occasionalmente una individuale, che lavora come l'agente finale tra una casa di produzione o alcuni agenti intermediari, ed un esercente, con il fine di assicurare le proiezioni del film del produttore sullo schermo della sala cinematografica. Nel campo del cinema, il termine "distribuzione" si riferisce al mercato e alla circolazione di film nei cinema.

In teoria delle probabilità la distribuzione Gamma è una distribuzione di probabilità continua, che comprende, come casi particolari, anche le distribuzioni esponenziale e chi quadrato. Viene utilizzata come modello generale dei tempi di attesa nella teoria delle code, soprattutto qualora siano importanti effetti che rimuovano "l'assenza di memoria" della distribuzione esponenziale. Nella statistica bayesiana è comune sia come distribuzione a priori che come distribuzione a posteriori.

Gli organi di distribuzione o più semplicemente distribuzione sono l'insieme degli organi meccanici predisposti al controllo dei gas che entrano ed escono nei cilindri. Esso lavora dunque accoppiato al sistema di alimentazione che lo comanda in funzione delle esigenze di motricità del veicolo. Questo sistema è usato sui motori a quattro tempi, sui motori a sei tempi e parte dei motori a due tempi unidirezionali.