La distribuzione normale (o distribuzione di Gauss dal nome del matematico tedesco Carl Friedrich Gauss), nella teoria della probabilità, è una distribuzione di probabilità continua che è spesso usata come prima approssimazione per descrivere variabili casuali a valori reali che tendono a concentrarsi attorno a un singolo valor medio. Il grafico della funzione di densità di probabilità associata è simmetrico e ha una forma a campana, nota come campana di Gauss (o anche come curva degli errori, curva a campana, ogiva).

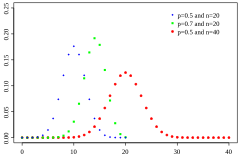
In teoria della probabilità la distribuzione binomiale è una distribuzione di probabilità discreta che descrive il numero di successi in un processo di Bernoulli, ovvero la variabile aleatoria S n = X 1 + X 2 + ⋯ + X n {\displaystyle S_{n}=X_{1}+X_{2}+\dotsb +X_{n}} che somma n {\displaystyle n} variabili aleatorie indipendenti di uguale distribuzione di Bernoulli B ( p ) {\displaystyle {\mathcal {B}}(p)} . Esempi di casi di distribuzione binomiale sono i risultati di una serie di lanci di una stessa moneta o di una serie di estrazioni da un'urna (con reintroduzione), ognuna delle quali può fornire due soli risultati: il successo con probabilità p {\displaystyle p} e il fallimento con probabilità q = 1 − p {\displaystyle q=1-p} .

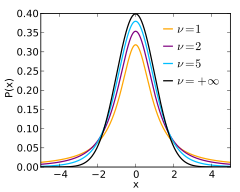
Nella teoria delle probabilità la distribuzione di Student, o t di Student, è una distribuzione di probabilità continua che governa il rapporto tra due variabili aleatorie, la prima con distribuzione normale e la seconda, al quadrato, segue una distribuzione chi quadrato. Questa distribuzione interviene nella stima della media di una popolazione che segue la distribuzione normale, e viene utilizzata negli omonimi test t di Student per la significatività e per ogni intervallo di confidenza della differenza tra due medie.

In teoria delle probabilità la distribuzione di Poisson (o poissoniana) è una distribuzione di probabilità discreta che esprime le probabilità per il numero di eventi che si verificano successivamente ed indipendentemente in un dato intervallo di tempo, sapendo che mediamente se ne verifica un numero λ {\displaystyle \lambda } . Ad esempio, si utilizza una distribuzione di Poisson per misurare il numero di chiamate ricevute in un call-center in un determinato arco temporale, come una mattinata lavorativa. Questa distribuzione è anche nota come legge degli eventi rari. Prende il nome dal matematico francese Siméon-Denis Poisson.

In teoria delle probabilità la distribuzione Gamma è una distribuzione di probabilità continua, che comprende, come casi particolari, anche le distribuzioni esponenziale e chi quadrato. Viene utilizzata come modello generale dei tempi di attesa nella teoria delle code, soprattutto qualora siano importanti effetti che rimuovano "l'assenza di memoria" della distribuzione esponenziale. Nella statistica bayesiana è comune sia come distribuzione a priori che come distribuzione a posteriori.