biblio toscana

In matematica, il limite di una funzione in un punto x 0 {\displaystyle x_{0}} di accumulazione per il suo dominio è un modo per esprimere la quantità a cui tende il valore assunto dalla funzione all'avvicinarsi del suo argomento a x 0 {\displaystyle x_{0}} . Indicando con f ( x ) {\displaystyle f(x)} la funzione, il limite viene indicato con la notazione: lim x → x 0 f ( x ) {\displaystyle \lim _{x\to x_{0}}f(x)} In altri termini, lim x → x 0 f ( x ) = l {\displaystyle \lim _{x\to x_{0}}f(x)=l} significa che quando il valore di x {\displaystyle x} si avvicina a x 0 {\displaystyle x_{0}} , esprimibile con x → x 0 {\displaystyle x\to x_{0}} , il valore f ( x ) {\displaystyle f(x)} assunto dalla funzione si avvicina a l {\displaystyle l} , cioè f ( x ) → l {\displaystyle f(x)\to l} . Il valore l {\displaystyle l} può essere finito ( l ∈ R {\displaystyle l\in \mathbb {R} } ), infinito ( ± ∞ {\displaystyle \pm \infty } ) o non esistere affatto. Il limite rappresenta in un certo senso il comportamento di un oggetto matematico quando una o più variabili del suo dominio tendono ad assumere un determinato valore. Il concetto di limite di una funzione viene generalizzato da quello di limite di un filtro, mentre un caso particolare è quello di limite di una successione di punti in uno spazio topologico.

In matematica, una funzione continua è una funzione che, intuitivamente, fa corrispondere ad elementi sufficientemente vicini del dominio elementi arbitrariamente vicini del codominio. Esistono diverse definizioni di continuità, corrispondenti ai contesti matematici in cui vengono utilizzate: la continuità di una funzione è uno dei concetti di base della topologia e dell'analisi matematica. La continuità di una funzione può essere definita anche in modo locale: in questo caso si parla di continuità in un punto del dominio. Una funzione continua è, per definizione, continua in ogni punto del proprio dominio. Una funzione che non è continua è detta discontinua, e i punti del dominio in cui non è continua sono detti punti di discontinuità. Per esempio, la funzione h(t) che descrive l'altezza di un uomo rispetto alla sua età può essere vista come una funzione continua: in periodi brevi l'uomo cresce di poco. Al contrario, la funzione g(t) che rappresenta la quantità di denaro presente in un conto corrente nel tempo è una funzione discontinua, poiché prelievi e depositi le fanno fare salti da un valore all'altro.

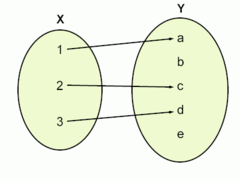
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).