biblio toscana

Nel calcolo differenziale vettoriale, il gradiente di una funzione a valori reali (ovvero di un campo scalare) è una funzione vettoriale. Il gradiente di una funzione è spesso definito come il vettore che ha come componenti le derivate parziali della funzione, anche se questo vale solo se si utilizzano coordinate cartesiane ortonormali. In generale, il gradiente di una funzione f {\displaystyle f} , denotato con ∇ f {\displaystyle \nabla f} (il simbolo ∇ {\displaystyle \nabla } si legge nabla), è definito in ciascun punto dalla seguente relazione: per un qualunque vettore v → {\displaystyle {\vec {v}}} , il prodotto scalare v → ⋅ ∇ f {\displaystyle {\vec {v}}\cdot \nabla f} dà il valore della derivata direzionale di f {\displaystyle f} rispetto a v → {\displaystyle {\vec {v}}} . In fisica, il gradiente di una grandezza scalare si usa per descrivere come quest'ultima vari in funzione dei suoi diversi parametri. Ad esempio, si parla di gradiente termico per esprimere la variazione della temperatura lungo una direzione scelta, o di gradiente di pressione, analogamente, per esprimere la variazione della pressione lungo una particolare direzione.

In matematica, una funzione continua è una funzione che, intuitivamente, fa corrispondere ad elementi sufficientemente vicini del dominio elementi arbitrariamente vicini del codominio. Esistono diverse definizioni di continuità, corrispondenti ai contesti matematici in cui vengono utilizzate: la continuità di una funzione è uno dei concetti di base della topologia e dell'analisi matematica. La continuità di una funzione può essere definita anche in modo locale: in questo caso si parla di continuità in un punto del dominio. Una funzione continua è, per definizione, continua in ogni punto del proprio dominio. Una funzione che non è continua è detta discontinua, e i punti del dominio in cui non è continua sono detti punti di discontinuità. Per esempio, la funzione h(t) che descrive l'altezza di un uomo rispetto alla sua età può essere vista come una funzione continua: in periodi brevi l'uomo cresce di poco. Al contrario, la funzione g(t) che rappresenta la quantità di denaro presente in un conto corrente nel tempo è una funzione discontinua, poiché prelievi e depositi le fanno fare salti da un valore all'altro.

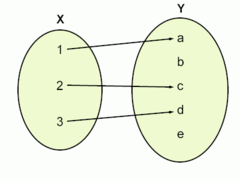
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).