In matematica un monomio è un'espressione algebrica costituita da un coefficiente e una parte letterale dove tra le lettere compaiono moltiplicazioni e elevamenti a potenza aventi esponente naturale. Questi sono tre esempi: 3 x , x 2 y , − x n . {\displaystyle 3x,\ x^{2}y,\ -x^{n}.} Nell'ultimo esempio, l'esponente n è un numero naturale non specificato. In alcuni casi si ammette la presenza nel monomio di esponenti negativi e si parla di monomi frazionari (o fratti): in questo caso, il monomio è in realtà una frazione algebrica: 2 x 2 y − 3 z = 2 x 2 z y 3 . {\displaystyle 2x^{2}y^{-3}z=2{\frac {x^{2}z}{y^{3}}}.} Talvolta si ammette anche l'operazione di estrazione di radice. I monomi con esponenti esclusivamente interi positivi sono detti interi e in questa voce ci limitiamo a considerare questo tipo di monomi. In un monomio non compaiono somme o sottrazioni; un'espressione del tipo x + 3 x y {\displaystyle x+3xy} dove compaiono anche delle somme algebriche è invece detta polinomio: un polinomio è quindi una somma algebrica di monomi.

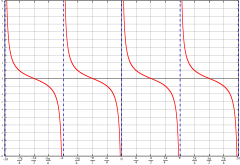
In matematica, in particolare in trigonometria, la cotangente di un angolo è definita come la proiezione sull'asse x {\displaystyle x} del punto di incontro tra il prolungamento del secondo lato dell'angolo orientato e la retta che tange la circonferenza goniometrica nel punto ( 0 ; 1 ) {\displaystyle (0;1)} . Spesso si usa definirla anche tramite il rapporto tra il coseno ed il seno dello stesso angolo: cot ⁡ x = cos ⁡ x sin ⁡ x {\displaystyle \cot x={\frac {\cos x}{\sin x}}} , oppure ricordando che la cotangente è il reciproco della tangente: cot ⁡ x = 1 tan ⁡ x . {\displaystyle \cot x={\frac {1}{\tan x}}.} In un triangolo rettangolo, la cotangente di un angolo acuto corrisponde al rapporto fra il cateto ad esso adiacente e quello opposto. Ne segue appunto che la cotangente è il reciproco della tangente. La cotangente è una funzione continua nel dominio ed è periodica con periodo minimo π {\displaystyle \pi } , cioè cot ⁡ x = cot ⁡ ( x + k π ) , k ∈ Z {\displaystyle \cot x=\cot(x+k\pi ),k\in \mathbb {Z} } . Non è una funzione limitata, né invertibile. Tuttavia se si restringe il dominio all'intervallo ( 0 , π ) {\displaystyle (0,\pi )} la funzione cotangente ristretta risulta invertibile in quanto strettamente monotona (in particolare strettamente decrescente) in tale intervallo. La sua derivata è d d x cot ⁡ x = − 1 sin 2 ⁡ x = − ( 1 + c o t 2 x ) {\displaystyle {\frac {d}{dx}}\cot x=-{\frac {1}{\sin ^{2}x}}=-(1+cot^{2}x)} , mentre la sua funzione primitiva è: ∫ cot ⁡ x d x = ln ⁡ | sen ⁡ x | + c . {\displaystyle \int \cot {x}\,\mathrm {d} x=\ln {\left|\operatorname {sen} {x}\right|+c}.} La funzione inversa della cotangente ristretta all'intervallo ( 0 , π ) {\displaystyle (0,\pi )} prende il nome di arcocotangente. Lo sviluppo di Taylor della funzione cotangente (qui arrestato al quinto ordine) è: cot ⁡ x = 1 x − x 3 − x 3 45 − 2 x 5 945 + o ( x 6 ) . {\displaystyle \cot x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}+o(x^{6}).} Inoltre la cotangente, essendo il reciproco della tangente che è una funzione dispari, è ancora una funzione dispari, e ciò comporta che: cot ⁡ ( − x ) = − cot ⁡ x . {\displaystyle \cot(-x)=-\cot {x}.} La seguente tabella elenca i principali valori notevoli della funzione cotangente: