biblio toscana

L'algebra lineare è la branca della matematica che si occupa dello studio dei vettori, spazi vettoriali (o spazi lineari), trasformazioni lineari e sistemi di equazioni lineari. Gli spazi vettoriali sono un tema centrale nella matematica moderna; l'algebra lineare è usata ampiamente nell'algebra astratta, nella geometria e nell'analisi funzionale. L'algebra lineare ha inoltre una rappresentazione concreta nella geometria analitica. Con l'algebra lineare si studiano completamente tutti i fenomeni fisici "lineari", cioè quelli in cui intuitivamente non entrano in gioco distorsioni, turbolenze e fenomeni caotici in generale. Anche fenomeni più complessi, non solo della fisica ma anche delle scienze naturali e sociali, possono essere studiati e ricondotti con le dovute approssimazioni a un modello lineare.

L'algebra di Boole (anche detta algebra booleana o reticolo booleano), in matematica e logica matematica, è il ramo dell'algebra in cui le variabili possono assumere solamente i valori vero e falso (valori di verità), generalmente denotati rispettivamente come 1 e 0.

L'algebra (dall'arabo الجبر, al-ğabr, 'completamento') è una branca della matematica che tratta lo studio di strutture algebriche, relazioni e quantità.

In algebra lineare, il determinante di una matrice quadrata A {\displaystyle A} è un numero che descrive alcune proprietà algebriche e geometriche della matrice. Esso viene generalmente indicato con det ( A ) {\displaystyle \det(A)} e, a volte, con | A | {\displaystyle |A|} . Quest'ultima notazione è più compatta, ma anche più ambigua, in quanto utilizzata talvolta per descrivere una norma della matrice.Il determinante è un potente strumento usato in vari settori della matematica: innanzitutto nello studio dei sistemi di equazioni lineari, quindi nel calcolo infinitesimale a più dimensioni (ad esempio nello Jacobiano), nel calcolo tensoriale, nella geometria differenziale, nella teoria combinatoria, ecc. Il significato geometrico principale del determinante si ottiene interpretando la matrice quadrata A {\displaystyle A} di ordine n {\displaystyle n} come trasformazione lineare di uno spazio vettoriale a n {\displaystyle n} dimensioni: con questa interpretazione, il valore assoluto di det ( A ) {\displaystyle \det(A)} è il fattore con cui vengono modificati i volumi degli oggetti contenuti nello spazio (anche se ciò è improprio senza considerare il significato di misura). Se è diverso da zero, il segno del determinante indica inoltre se la trasformazione A {\displaystyle A} preserva o cambia l'orientazione dello spazio rispetto agli assi di riferimento.

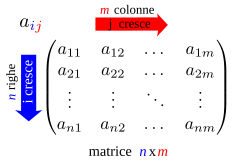
In matematica, in particolare in algebra lineare, una matrice è una tabella ordinata di elementi. Ad esempio: ( 1 0 5 1 − 2 0 ) {\displaystyle {\begin{pmatrix}1&0&5\\1&-2&0\end{pmatrix}}} Le matrici sono ampiamente usate in matematica e in tutte le scienze per la loro capacità di rappresentare in maniera utile e concisa diversi oggetti matematici, come valori che dipendono da due parametri o anche sistemi lineari, cosa, quest'ultima, che le rende uno strumento centrale dell'analisi matematica.