- Libri preferiti
Accedi all'area personale per aggiungere e visualizzare i tuoi libri preferiti
Accedi all'area personale per aggiungere e visualizzare i tuoi libri preferiti
L'algebra di Boole (anche detta algebra booleana o reticolo booleano), in matematica e logica matematica, è il ramo dell'algebra in cui le variabili possono assumere solamente i valori vero e falso (valori di verità), generalmente denotati rispettivamente come 1 e 0.
In matematica, una σ-algebra (pronunciata sigma-algebra) o tribù (termine introdotto dal gruppo Bourbaki) su di un insieme Ω {\displaystyle \Omega } , è una famiglia di sottoinsiemi di Ω {\displaystyle \Omega } che ha delle proprietà di chiusura rispetto ad alcune operazioni insiemistiche, in particolare l'operazione di unione numerabile e di passaggio al complementare. La struttura di σ-algebra è particolarmente utile nelle teorie della misura e probabilità ed è alla base di tutte le nozioni di misurabilità, sia di insiemi che di funzioni. Essa è un caso particolare di algebra di insiemi e, rispetto a quest'ultima, è utilizzata molto più ampiamente in Analisi (per via delle numerose proprietà che le misure definite su σ-algebre hanno rispetto alle operazioni di passaggio al limite). Le σ-algebre che ricorrono più spesso in matematica sono le σ-algebre boreliane e la σ-algebra di Lebesgue. Anche storicamente queste due classi di σ-algebre hanno motivato lo sviluppo del concetto stesso di σ-algebra, nato a cavallo di XIX secolo e XX secolo col fine di formalizzare la teoria della misura. Esso, infatti, precisa l'idea euristica di evento o insieme misurabile. Molte importanti strutture astratte, al centro dei progressi della matematica dell'ultimo secolo, sono definibili mediante σ-algebre.

In algebra lineare, il determinante di una matrice quadrata A {\displaystyle A} è un numero che descrive alcune proprietà algebriche e geometriche della matrice. Esso viene generalmente indicato con det ( A ) {\displaystyle \det(A)} e, a volte, con | A | {\displaystyle |A|} . Quest'ultima notazione è più compatta, ma anche più ambigua, in quanto utilizzata talvolta per descrivere una norma della matrice.Il determinante è un potente strumento usato in vari settori della matematica: innanzitutto nello studio dei sistemi di equazioni lineari, quindi nel calcolo infinitesimale a più dimensioni (ad esempio nello Jacobiano), nel calcolo tensoriale, nella geometria differenziale, nella teoria combinatoria, ecc. Il significato geometrico principale del determinante si ottiene interpretando la matrice quadrata A {\displaystyle A} di ordine n {\displaystyle n} come trasformazione lineare di uno spazio vettoriale a n {\displaystyle n} dimensioni: con questa interpretazione, il valore assoluto di det ( A ) {\displaystyle \det(A)} è il fattore con cui vengono modificati i volumi degli oggetti contenuti nello spazio (anche se ciò è improprio senza considerare il significato di misura). Se è diverso da zero, il segno del determinante indica inoltre se la trasformazione A {\displaystyle A} preserva o cambia l'orientazione dello spazio rispetto agli assi di riferimento.

La topologia (dal greco τόπος, tópos, "luogo", e λόγος, lógos, "studio", col significato quindi di "studio dei luoghi'") è una branca della geometria che studia le proprietà delle figure, e in generale degli oggetti matematici, che non cambiano quando viene effettuata una deformazione senza "strappi", "sovrapposizioni" o "incollature". È una delle più importanti branche della matematica moderna. Concetti fondamentali come convergenza, limite, continuità, connessione o compattezza trovano nella topologia la loro migliore formalizzazione. Si basa essenzialmente sui concetti di spazio topologico, funzione continua e omeomorfismo. Col termine topologia si indica anche la collezione di aperti che definisce uno spazio topologico. Per esempio un cubo e una sfera sono oggetti topologicamente equivalenti (cioè omeomorfi), perché possono essere deformati l'uno nell'altro senza ricorrere ad alcuna incollatura, strappo o sovrapposizione; una sfera e un toro invece non lo sono, perché il toro contiene un "buco" che non può essere eliminato da una deformazione.
In matematica, in particolare nel calcolo vettoriale, il prodotto vettoriale è un'operazione binaria interna tra due vettori in uno spazio euclideo tridimensionale che restituisce un altro vettore che è normale al piano formato dai vettori di partenza. Il prodotto vettoriale è indicato con il simbolo × {\displaystyle \times } o con il simbolo ∧ {\displaystyle \wedge } . Il secondo simbolo è però anche usato per indicare il prodotto esterno (o prodotto wedge) nell'algebra di Grassmann, di Clifford e nelle forme differenziali. Storicamente, il prodotto esterno è stato definito da Grassmann circa trent'anni prima che Gibbs e Heaviside definissero il prodotto vettoriale.
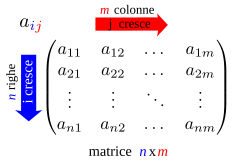
In matematica, in particolare in algebra lineare, una matrice è una tabella ordinata di elementi. Ad esempio: ( 1 0 5 1 − 2 0 ) {\displaystyle {\begin{pmatrix}1&0&5\\1&-2&0\end{pmatrix}}} Le matrici sono ampiamente usate in matematica e in tutte le scienze per la loro capacità di rappresentare in maniera utile e concisa diversi oggetti matematici, come valori che dipendono da due parametri o anche sistemi lineari, cosa, quest'ultima, che le rende uno strumento centrale dell'analisi matematica.
In matematica, e più precisamente in algebra lineare, una applicazione multilineare è una funzione che generalizza il concetto di applicazione lineare a più variabili. Esempi classici di applicazioni multilineari sono: una applicazione lineare, il determinante e la traccia, un prodotto scalare o una più generale forma bilineare.Le applicazioni multilineari sono anche alla base della definizione di tensore e forma differenziale, e sono quindi molto usate in topologia differenziale nello studio delle varietà differenziabili. Hanno in particolare importanti applicazioni in fisica, specialmente in relatività generale. Sono sinonimi i termini funzione e mappa multilineare.
L'algebra di Grassmann o algebra esterna di un dato spazio vettoriale V {\displaystyle V} sopra un campo K {\displaystyle K} è una certa algebra associativa dotata di elemento neutro, generata dalla definizione di un prodotto esterno o prodotto wedge scritto come ∧ {\displaystyle \wedge } . È denotata con ( Λ ( V ) , ∧ ) {\displaystyle \left(\Lambda (V),\,\wedge \right)} e contiene V {\displaystyle V} come sottospazio. Le algebre esterne sono molto utilizzate nella geometria differenziale e nella geometria algebrica (algebra esterna delle forme differenziali) oltre che nell'algebra multilineare e nei settori collegati. Il prodotto esterno è associativo e bilineare; la sua proprietà essenziale è che sia alternante su V {\displaystyle V} : v ∧ v = 0 {\displaystyle v\wedge v=0} per tutti i vettori v ∈ V {\displaystyle v\in V} ossia: u ∧ v = − v ∧ u {\displaystyle u\wedge v=-v\wedge u} per ogni vettore u , v ∈ V {\displaystyle u,v\in V} , e v 1 ∧ v 2 ∧ ⋯ ∧ v k = 0 {\displaystyle v_{1}\wedge v_{2}\wedge \cdots \wedge v_{k}=0} qualora v 1 , … , v k ∈ V {\displaystyle v_{1},\ldots ,v_{k}\in V} siano linearmente dipendenti.Il concetto di prodotto esterno generalizza i concetti di prodotto vettoriale e di triplo prodotto scalare della geometria euclidea tridimensionale. Esso fornisce un modo algebrico astratto, indipendente dalla scelta di una base, per descrivere il determinante e i minori di una trasformazione lineare. È quindi collegato alle idee di indipendenza lineare e di rango. L'algebra di Grassmann è l'esempio prototipo di algebre supercommutative. Queste sono algebre con una decomposizione in variabili pari e dispari che soddisfa una versione graduata della commutatività (in particolare, elementi dispari anticommutano).