La trigonometria (dal greco trígonon (τρίγωνον, triangolo) e métron (μέτρον, misura): risoluzione del triangolo) è la parte della matematica che studia i triangoli a partire dai loro angoli. Il compito principale della trigonometria, così come rivela l'etimologia del nome, consiste nel calcolare le misure che caratterizzano gli elementi di un triangolo (lati, angoli, mediane, etc.) partendo da altre misure già note (almeno tre, di cui almeno una lunghezza), per mezzo di speciali funzioni. Tale compito è indicato come risoluzione del triangolo. È anche possibile servirsi di calcoli trigonometrici nella risoluzione di problemi correlati a figure geometriche più complesse, come poligoni o figure geometriche solide, ed in molti altri rami della matematica. Le funzioni trigonometriche (le più importanti delle quali sono il seno e il coseno), introdotte in questo ambito, vengono anche usate in maniera indipendente dalla geometria, comparendo anche in altri campi della matematica e delle sue applicazioni, ad esempio in connessione con la funzione esponenziale o con le operazioni vettoriali.

In matematica, la secante di un angolo è una funzione trigonometrica definita come il reciproco del coseno dello stesso angolo, ossia: sec ⁡ α = 1 cos ⁡ α . {\displaystyle \sec \alpha ={\frac {1}{\cos \alpha }}.}

In matematica, le funzioni trigonometriche o funzioni goniometriche o funzioni circolari sono funzioni di un angolo; esse sono importanti nello studio dei triangoli e nella modellizzazione dei fenomeni periodici, oltre a un gran numero di altre applicazioni. Sono spesso definite come rapporti fra i lati di un triangolo rettangolo contenenti l'angolo e, equivalentemente, possono essere definite come le lunghezze di diversi segmenti costruiti dal cerchio unitario. Definizioni più moderne li esprimono come serie infinite o come soluzioni di certe equazioni differenziali, ottenendo la loro estensione a valori positivi o negativi e anche ai numeri complessi. Tutti questi differenti approcci sono presentati di seguito. Lo studio delle funzioni trigonometriche risale ai tempi dei babilonesi, e una quantità considerevole del lavoro fondamentale fu svolto dai matematici greci, indiani e persiani. Nell'uso corrente, vi sono sei funzioni trigonometriche di base, che sono elencate sotto insieme alle identità che le mettono in relazione. Specialmente per le ultime quattro, queste relazioni sono spesso prese come definizioni di quelle funzioni, sebbene sia ugualmente possibile definirle geometricamente o per altre vie, e solo in seguito derivare queste relazioni. Poche altre funzioni erano comuni in passato (e figuravano nelle vecchie tabelle) ma sono oggi poco usate, come il senoverso (1 − cos θ) e l'exsecante (sec θ − 1). Molte altre relazioni notevoli fra queste funzioni sono elencate nella voce sulle identità trigonometriche.

I Lineamenti di filosofia del diritto, pubblicati a Berlino nel 1820 (pur riportando la data del 1821) rappresentano la sintesi complessiva del pensiero etico-politico di Hegel. Con quest'ultima opera pubblicata con il sottotitolo Diritto naturale e scienza dello Stato in compendio, l'autore espone gli aspetti fondamentali dello sviluppo dialettico dell'Idea che mira a «comprendere concettualmente lo Stato e di esporlo come qualcosa di intimamente razionale».

La geometria (dal latino geometrĭa e questo dal greco antico "γεωμετρία", composto dal prefisso geo che rimanda alla parola γή = "terra" e μετρία, metria = "misura", tradotto quindi letteralmente come misurazione della terra) è quella parte della scienza matematica che si occupa delle forme nel piano e nello spazio e delle loro mutue relazioni.

Federigo Enriques (Livorno, 5 gennaio 1871 – Roma, 14 giugno 1946) è stato un matematico, storico della scienza e filosofo italiano.

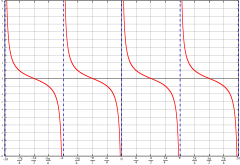
In matematica, in particolare in trigonometria, la cotangente di un angolo è definita come la proiezione sull'asse x {\displaystyle x} del punto di incontro tra il prolungamento del secondo lato dell'angolo orientato e la retta che tange la circonferenza goniometrica nel punto ( 0 ; 1 ) {\displaystyle (0;1)} . Spesso si usa definirla anche tramite il rapporto tra il coseno ed il seno dello stesso angolo: cot ⁡ x = cos ⁡ x sin ⁡ x {\displaystyle \cot x={\frac {\cos x}{\sin x}}} , oppure ricordando che la cotangente è il reciproco della tangente: cot ⁡ x = 1 tan ⁡ x . {\displaystyle \cot x={\frac {1}{\tan x}}.} In un triangolo rettangolo, la cotangente di un angolo acuto corrisponde al rapporto fra il cateto ad esso adiacente e quello opposto. Ne segue appunto che la cotangente è il reciproco della tangente. La cotangente è una funzione continua nel dominio ed è periodica con periodo minimo π {\displaystyle \pi } , cioè cot ⁡ x = cot ⁡ ( x + k π ) , k ∈ Z {\displaystyle \cot x=\cot(x+k\pi ),k\in \mathbb {Z} } . Non è una funzione limitata, né invertibile. Tuttavia se si restringe il dominio all'intervallo ( 0 , π ) {\displaystyle (0,\pi )} la funzione cotangente ristretta risulta invertibile in quanto strettamente monotona (in particolare strettamente decrescente) in tale intervallo. La sua derivata è d d x cot ⁡ x = − 1 sin 2 ⁡ x = − ( 1 + c o t 2 x ) {\displaystyle {\frac {d}{dx}}\cot x=-{\frac {1}{\sin ^{2}x}}=-(1+cot^{2}x)} , mentre la sua funzione primitiva è: ∫ cot ⁡ x d x = ln ⁡ | sen ⁡ x | + c . {\displaystyle \int \cot {x}\,\mathrm {d} x=\ln {\left|\operatorname {sen} {x}\right|+c}.} La funzione inversa della cotangente ristretta all'intervallo ( 0 , π ) {\displaystyle (0,\pi )} prende il nome di arcocotangente. Lo sviluppo di Taylor della funzione cotangente (qui arrestato al quinto ordine) è: cot ⁡ x = 1 x − x 3 − x 3 45 − 2 x 5 945 + o ( x 6 ) . {\displaystyle \cot x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}+o(x^{6}).} Inoltre la cotangente, essendo il reciproco della tangente che è una funzione dispari, è ancora una funzione dispari, e ciò comporta che: cot ⁡ ( − x ) = − cot ⁡ x . {\displaystyle \cot(-x)=-\cot {x}.} La seguente tabella elenca i principali valori notevoli della funzione cotangente:

L'arbitrato (dal latino arbitratus, lett. "giudizio") è un metodo alternativo di risoluzione delle controversie (cioè senza ricorso ad un procedimento giudiziario), che consiste nell'affidamento a uno o più soggetti terzi (gli arbitri) dell'incarico di risolvere una controversia, mediante una decisione (il lodo) che sarà vincolante per le parti e suscettibile di essere eseguita, anche in via forzata.

L'analisi matematica è il ramo della matematica che si occupa delle proprietà che emergono dalla scomposizione infinita di un oggetto denso. Si fonda sul calcolo infinitesimale, con il quale, attraverso le nozioni di limite e continuità, studia il comportamento locale di una funzione utilizzando gli strumenti del calcolo differenziale e del calcolo integrale. Introducendo per il calcolo concetti problematici, quali quello di infinito e di limite, si può passare all'indagine che le ha permesso di divenire basilare in diverse discipline scientifiche e tecniche (dalle scienze naturali all'ingegneria, dall'informatica all'economia), dove viene spesso coniugata con l'analisi numerica.