biblio toscana

L'analisi armonica è la branca dell'analisi matematica che studia la rappresentazione delle funzioni o dei segnali come sovrapposizione di onde o fondamentali. Tali onde fondamentali sono chiamate "armoniche", da cui il nome "analisi armonica". Essa dunque indaga e generalizza la nozione di serie di Fourier e trasformata di Fourier. Nei precedenti due secoli è diventato un tema molto vasto con applicazioni in diverse aree come elaborazione numerica dei segnali, meccanica quantistica e neuroscienze. La classica trasformata di Fourier su R n {\displaystyle \mathbb {R} ^{n}} è ancora oggetto di ricerca, in particolare la trasformazione di Fourier di oggetti più generali come le distribuzioni temperate. Ad esempio, se si impongono alcuni requisiti a una distribuzione f {\displaystyle f} , si può cercare di tradurre questi requisiti in termini della trasformata di Fourier di f {\displaystyle f} . Il teorema di Paley-Wiener è un esempio di questo. Il teorema di Paley-Wiener implica immediatamente che se f {\displaystyle f} è una distribuzione non nulla di supporto compatto (questa definizione include le funzioni di supporto compatto), allora la sua trasformata di Fourier non ha mai supporto compatto. Questa è una forma molto elementare di principio di indeterminazione nell'ambito dell'analisi armonica. Le serie di Fourier possono essere agevolmente studiate nel contesto degli spazi di Hilbert, che offre un collegamento fra analisi armonica e analisi funzionale.

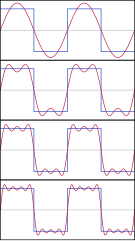
In matematica, in particolare in analisi armonica, la serie di Fourier è una rappresentazione di una funzione periodica mediante una combinazione lineare di funzioni sinusoidali. Questo tipo di decomposizione è alla base dell'analisi di Fourier.

Il reddito di base o reddito di cittadinanza o reddito minimo universale è un'erogazione monetaria, a intervallo di tempo regolare, distribuita a tutte le persone dotate di cittadinanza e di residenza, cumulabile con altri redditi (da lavoro, da impresa, da rendita), indipendentemente dall'attività lavorativa effettuata o non effettuata (dunque viene erogata sia ai lavoratori sia ai disoccupati), dal sesso, dal credo religioso e dalla posizione sociale, ed erogato durante tutta la vita del soggetto.

In matematica il termine operatore viene usato in vari contesti con significati che presentano alcune diversità, ma che in ogni caso si collegano alla nozione di funzione.

Con il termine falansterio il filosofo e politologo francese Charles Fourier, agli inizi del XIX secolo, indicava la struttura abitativa in cui si svolgeva la vita dei membri dell'unità sociale di base prevista nelle sue teorie e da lui denominata "Falange".

François Marie Charles Fourier (Besançon, 7 aprile 1772 – Parigi, 10 ottobre 1837) è stato un filosofo francese, che ispirò la fondazione della comunità socialista utopista chiamata La Reunion sorta presso l'attuale Dallas in Texas, oltre a diverse altre comunità negli Stati Uniti d'America (tra le quali ricordiamo Brook Farm, fondata nel 1841 vicino Boston e sciolta a seguito d'un incendio, nel 1849).

L'analisi numerica (detta anche calcolo numerico o calcolo scientifico) è una branca della matematica applicata che risolve i modelli prodotti dall'analisi matematica alle scomposizioni finite normalmente praticabili, coinvolgendo il concetto di approssimazione. I suoi strumenti, detti algoritmi, sono caratterizzabili in base a velocità di convergenza, stabilità numerica e computabilità.

L'analisi funzionale è il settore dell'analisi matematica che si occupa dello studio di spazi di funzioni. Affonda le sue radici storiche nello studio delle trasformate come la trasformata di Fourier e nello studio delle equazioni differenziali e integrali. La parola "funzionale" viene dal calcolo delle variazioni, e indica una funzione il cui argomento è una funzione. Il suo uso in senso più generale è attribuito a Vito Volterra.

In analisi matematica, l'analisi di Fourier, nota anche come analisi armonica, è una branca di ricerca che ha preso avvio dalle ricerche di Jean Baptiste Joseph Fourier che, nei primi anni dell'Ottocento, riuscì a dimostrare matematicamente come una qualunque funzione periodica poteva essere scomposta in una somma di infinite "opportune" funzioni o componenti sinusoidali (seno e coseno) dette armoniche. Da tale constatazione nasce dunque l'idea di scomporre funzioni complicate in una serie di funzioni, nota come serie di Fourier, rendendone l'analisi più semplice e vantaggiosa. Dal concetto matematico di serie di Fourier discende anche la nozione di trasformata di Fourier ed il relativo concetto associato di dominio della frequenza.