- Libri preferiti
Accedi all'area personale per aggiungere e visualizzare i tuoi libri preferiti
Accedi all'area personale per aggiungere e visualizzare i tuoi libri preferiti
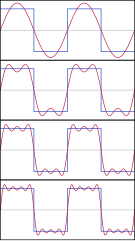
In matematica, in particolare in analisi armonica, la serie di Fourier è una rappresentazione di una funzione periodica mediante una combinazione lineare di funzioni sinusoidali. Questo tipo di decomposizione è alla base dell'analisi di Fourier.
Il V postulato di Euclide è il postulato più conosciuto fra quelli che il matematico Euclide enuncia nei suoi Elementi. I matematici si sono cimentati per più di duemila anni nel tentativo di dedurlo dai primi quattro postulati, finché nell'Ottocento hanno effettivamente dimostrato la sua indeducibilità. Modificando questo postulato si creano geometrie diverse, dette non euclidee.
In matematica, in particolare nell'analisi di Fourier, la trasformata discreta di Fourier, anche detta DFT (acronimo del termine inglese Discrete Fourier Transform), è un particolare tipo di trasformata di Fourier. Si tratta anche di un caso particolare della trasformata zeta. Si tratta di una trasformata che converte una collezione finita di campioni equispaziati di una funzione in una collezione di coefficienti di una combinazione lineare di sinusoidi complesse, ordinate al crescere della frequenza. Analogamente alla trasformata di Fourier, si tratta di un modo per rappresentare una funzione (la cui variabile è spesso il tempo) nel dominio delle frequenze. Le frequenze delle sinusoidi della combinazione lineare (periodica) prodotta dalla trasformata sono multipli interi di una frequenza fondamentale, il cui periodo è la lunghezza dell'intervallo di campionamento. Si differenzia dalla trasformata di Fourier a tempo discreto per il fatto che la funzione in ingresso e la funzione prodotta sono successioni finite, e può essere quindi considerata come una trasformata per l'analisi di Fourier di funzioni su un dominio limitato e discreto. Diversamente dalla trasformata continua di Fourier, pertanto, la DFT richiede in ingresso una funzione discreta i cui valori sono in generale complessi e non nulli, ed hanno una durata limitata. Questo rende la DFT ideale per l'elaborazione di informazioni su un elaboratore elettronico. In particolare la trasformata discreta di Fourier è ampiamente utilizzata nel campo dell'elaborazione numerica dei segnali e nei campi correlati per analizzare le frequenze contenute in un segnale, per risolvere equazioni differenziali alle derivate parziali e per compiere altre operazioni, come la convoluzione o la moltiplicazione di numeri interi molto grandi. Alla base di questi utilizzi c'è la possibilità di calcolare in modo efficiente la DFT usando gli algoritmi per trasformata di Fourier veloce.
In analisi matematica, la trasformata di Fourier è una trasformata integrale, cioè un operatore che trasforma una funzione in un'altra funzione, sviluppata dal matematico francese Jean Baptiste Joseph Fourier nel 1822, nel suo trattato Théorie analytique de la chaleur, con numerose applicazioni nella fisica e nell'ingegneria ovvero uno degli strumenti matematici maggiormente utilizzati nell'ambito delle scienze pure e applicate, permettendo di scrivere una funzione dipendente dal tempo nel dominio delle frequenze, grazie alla decomposizione della funzione nella base delle funzioni esponenziali con un prodotto scalare, rappresentazione spesso chiamata spettro della funzione (il nome non ha nulla a che fare con l'omonimo concetto di spettro di un operatore). A volte si intende per trasformata di Fourier la funzione che risulta dall'applicazione di questo operatore.

Una stella è un corpo celeste che brilla di luce propria. In astronomia e astrofisica il termine indica uno sferoide luminoso di plasma che genera energia nel proprio nucleo attraverso processi di fusione nucleare; tale energia è irradiata nello spazio sotto forma di radiazione elettromagnetica, flusso di particelle elementari (vento stellare) e neutrini. Buona parte degli elementi chimici più pesanti dell'idrogeno e dell'elio (i più abbondanti nell'Universo) vengono sintetizzati nei nuclei delle stelle tramite il processo di nucleosintesi. La stella più vicina alla Terra è il Sole, sorgente di gran parte dell'energia del nostro pianeta. Le altre stelle, ad eccezione di alcune supernove, sono visibili solamente durante la notte come dei puntini luminosi, che appaiono tremolanti a causa degli effetti distorsivi (seeing) operati dall'atmosfera terrestre.Le stelle sono oggetti dotati di una massa considerevole, compresa tra 0,08 e 150–200 masse solari (M☉). Gli oggetti con una massa inferiore a 0,08 M☉ sono detti nane brune, corpi a metà strada tra stelle e pianeti che non producono energia tramite la fusione nucleare, mentre non sembrano esistere, almeno apparentemente, stelle di massa superiore a 200 M☉, per via del limite di Eddington. Sono variabili anche le dimensioni, comprese tra i pochi km delle stelle degeneri e i miliardi di km delle supergiganti e ipergiganti, e le luminosità, comprese tra 10−4 e 106 - 107 luminosità solari (L☉). Le stelle si presentano, oltre che singolarmente, anche in sistemi costituiti da due (stelle binarie) o più componenti (sistemi multipli), legate dalla forza di gravità. Un buon numero di stelle convive in associazioni o ammassi stellari (suddivisi in aperti e globulari), a loro volta raggruppati, insieme a stelle singole e nubi di gas e polveri, in addensamenti ancora più estesi, che prendono il nome di galassie. Numerose stelle possiedono inoltre uno stuolo più o meno ampio di pianeti.Nel corso della storia numerosi filosofi, poeti, scrittori e musicisti si sono ispirati al cielo stellato per la realizzazione delle loro opere e, in diversi casi, si sono interessati direttamente allo studio dell'astronomia. Le stelle sono divise in classi di magnitudine o grandezza apparente. La regola dice " quanto più debole è la stella, tanto maggiore è il numero esprimente la grandezza", così le stelle di terza grandezza sono più deboli di quelle di seconda grandezza e le stelle di prima grandezza sono cento volte più luminose di quelle più deboli visibili senza telescopio (sesta grandezza). La Via Lattea, la nostra galassia, contiene oltre 100 miliardi di stelle. Alcune più piccole e meno luminose del Sole, altre, come le nane bianche, non più grandi della Terra; ma ve ne sono alcune di gigantesche, come Betelgeuse, il cui diametro è maggiore di quello dell'orbita della Terra intorno al Sole.

Con il termine moto browniano si fa riferimento al moto disordinato di particelle sufficientemente piccole (aventi diametro dell'ordine del micrometro) da essere sottoposte a una forza di gravità trascurabile, presenti in fluidi o sospensioni fluide o gassose (ad esempio il fumo), ed osservabile al microscopio. Il fenomeno fu scoperto agli inizi dell'Ottocento dal botanico scozzese Robert Brown, e modellizzato nel 1905 dal fisico teorico tedesco Albert Einstein.Il termine viene usato per indicare sia il fenomeno naturale sia la sua rappresentazione matematica, la quale può descrivere l'andamento temporale di una classe molto ampia di fenomeni casuali. Un'importante categoria di fenomeni rappresentabili con gli strumenti matematici del moto browniano è costituita dall'andamento dei mercati finanziari, come dimostrato sin dal 1900 dal matematico francese Louis Bachelier, nel suo lavoro Théorie de la spéculation.

L'analisi matematica è il ramo della matematica che si occupa delle proprietà che emergono dalla scomposizione infinita di un oggetto denso. Si fonda sul calcolo infinitesimale, con il quale, attraverso le nozioni di limite e continuità, studia il comportamento locale di una funzione utilizzando gli strumenti del calcolo differenziale e del calcolo integrale. Introducendo per il calcolo concetti problematici, quali quello di infinito e di limite, si può passare all'indagine che le ha permesso di divenire basilare in diverse discipline scientifiche e tecniche (dalle scienze naturali all'ingegneria, dall'informatica all'economia), dove viene spesso coniugata con l'analisi numerica.
L'analisi armonica è la branca dell'analisi matematica che studia la rappresentazione delle funzioni o dei segnali come sovrapposizione di onde o fondamentali. Tali onde fondamentali sono chiamate "armoniche", da cui il nome "analisi armonica". Essa dunque indaga e generalizza la nozione di serie di Fourier e trasformata di Fourier. Nei precedenti due secoli è diventato un tema molto vasto con applicazioni in diverse aree come elaborazione numerica dei segnali, meccanica quantistica e neuroscienze. La classica trasformata di Fourier su R n {\displaystyle \mathbb {R} ^{n}} è ancora oggetto di ricerca, in particolare la trasformazione di Fourier di oggetti più generali come le distribuzioni temperate. Ad esempio, se si impongono alcuni requisiti a una distribuzione f {\displaystyle f} , si può cercare di tradurre questi requisiti in termini della trasformata di Fourier di f {\displaystyle f} . Il teorema di Paley-Wiener è un esempio di questo. Il teorema di Paley-Wiener implica immediatamente che se f {\displaystyle f} è una distribuzione non nulla di supporto compatto (questa definizione include le funzioni di supporto compatto), allora la sua trasformata di Fourier non ha mai supporto compatto. Questa è una forma molto elementare di principio di indeterminazione nell'ambito dell'analisi armonica. Le serie di Fourier possono essere agevolmente studiate nel contesto degli spazi di Hilbert, che offre un collegamento fra analisi armonica e analisi funzionale.