biblio toscana

In analisi matematica, la trasformata di Fourier è una trasformata integrale, cioè un operatore che trasforma una funzione in un'altra funzione, sviluppata dal matematico francese Jean Baptiste Joseph Fourier nel 1822, nel suo trattato Théorie analytique de la chaleur, con numerose applicazioni nella fisica e nell'ingegneria ovvero uno degli strumenti matematici maggiormente utilizzati nell'ambito delle scienze pure e applicate, permettendo di scrivere una funzione dipendente dal tempo nel dominio delle frequenze, grazie alla decomposizione della funzione nella base delle funzioni esponenziali con un prodotto scalare, rappresentazione spesso chiamata spettro della funzione (il nome non ha nulla a che fare con l'omonimo concetto di spettro di un operatore). A volte si intende per trasformata di Fourier la funzione che risulta dall'applicazione di questo operatore.

In matematica, in particolare nell'analisi di Fourier, la trasformata discreta di Fourier, anche detta DFT (acronimo del termine inglese Discrete Fourier Transform), è un particolare tipo di trasformata di Fourier. Si tratta anche di un caso particolare della trasformata zeta. Si tratta di una trasformata che converte una collezione finita di campioni equispaziati di una funzione in una collezione di coefficienti di una combinazione lineare di sinusoidi complesse, ordinate al crescere della frequenza. Analogamente alla trasformata di Fourier, si tratta di un modo per rappresentare una funzione (la cui variabile è spesso il tempo) nel dominio delle frequenze. Le frequenze delle sinusoidi della combinazione lineare (periodica) prodotta dalla trasformata sono multipli interi di una frequenza fondamentale, il cui periodo è la lunghezza dell'intervallo di campionamento. Si differenzia dalla trasformata di Fourier a tempo discreto per il fatto che la funzione in ingresso e la funzione prodotta sono successioni finite, e può essere quindi considerata come una trasformata per l'analisi di Fourier di funzioni su un dominio limitato e discreto. Diversamente dalla trasformata continua di Fourier, pertanto, la DFT richiede in ingresso una funzione discreta i cui valori sono in generale complessi e non nulli, ed hanno una durata limitata. Questo rende la DFT ideale per l'elaborazione di informazioni su un elaboratore elettronico. In particolare la trasformata discreta di Fourier è ampiamente utilizzata nel campo dell'elaborazione numerica dei segnali e nei campi correlati per analizzare le frequenze contenute in un segnale, per risolvere equazioni differenziali alle derivate parziali e per compiere altre operazioni, come la convoluzione o la moltiplicazione di numeri interi molto grandi. Alla base di questi utilizzi c'è la possibilità di calcolare in modo efficiente la DFT usando gli algoritmi per trasformata di Fourier veloce.

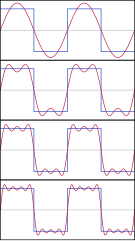
In matematica, in particolare in analisi armonica, la serie di Fourier è una rappresentazione di una funzione periodica mediante una combinazione lineare di funzioni sinusoidali. Questo tipo di decomposizione è alla base dell'analisi di Fourier.

In matematica il termine operatore viene usato in vari contesti con significati che presentano alcune diversità, ma che in ogni caso si collegano alla nozione di funzione.

L'analisi numerica (detta anche calcolo numerico o calcolo scientifico) è una branca della matematica applicata che risolve i modelli prodotti dall'analisi matematica alle scomposizioni finite normalmente praticabili, coinvolgendo il concetto di approssimazione. I suoi strumenti, detti algoritmi, sono caratterizzabili in base a velocità di convergenza, stabilità numerica e computabilità.

L'analisi funzionale è il settore dell'analisi matematica che si occupa dello studio di spazi di funzioni. Affonda le sue radici storiche nello studio delle trasformate come la trasformata di Fourier e nello studio delle equazioni differenziali e integrali. La parola "funzionale" viene dal calcolo delle variazioni, e indica una funzione il cui argomento è una funzione. Il suo uso in senso più generale è attribuito a Vito Volterra.

In analisi matematica, l'analisi di Fourier, nota anche come analisi armonica, è una branca di ricerca che ha preso avvio dalle ricerche di Jean Baptiste Joseph Fourier che, nei primi anni dell'Ottocento, riuscì a dimostrare matematicamente come una qualunque funzione periodica poteva essere scomposta in una somma di infinite "opportune" funzioni o componenti sinusoidali (seno e coseno) dette armoniche. Da tale constatazione nasce dunque l'idea di scomporre funzioni complicate in una serie di funzioni, nota come serie di Fourier, rendendone l'analisi più semplice e vantaggiosa. Dal concetto matematico di serie di Fourier discende anche la nozione di trasformata di Fourier ed il relativo concetto associato di dominio della frequenza.