biblio toscana

In analisi matematica, la trasformata di Fourier è una trasformata integrale, cioè un operatore che trasforma una funzione in un'altra funzione, sviluppata dal matematico francese Jean Baptiste Joseph Fourier nel 1822, nel suo trattato Théorie analytique de la chaleur, con numerose applicazioni nella fisica e nell'ingegneria ovvero uno degli strumenti matematici maggiormente utilizzati nell'ambito delle scienze pure e applicate, permettendo di scrivere una funzione dipendente dal tempo nel dominio delle frequenze, grazie alla decomposizione della funzione nella base delle funzioni esponenziali con un prodotto scalare, rappresentazione spesso chiamata spettro della funzione (il nome non ha nulla a che fare con l'omonimo concetto di spettro di un operatore). A volte si intende per trasformata di Fourier la funzione che risulta dall'applicazione di questo operatore.

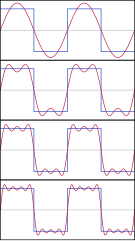
In matematica, in particolare in analisi armonica, la serie di Fourier è una rappresentazione di una funzione periodica mediante una combinazione lineare di funzioni sinusoidali. Questo tipo di decomposizione è alla base dell'analisi di Fourier.

In analisi matematica, l'analisi di Fourier, nota anche come analisi armonica, è una branca di ricerca che ha preso avvio dalle ricerche di Jean Baptiste Joseph Fourier che, nei primi anni dell'Ottocento, riuscì a dimostrare matematicamente come una qualunque funzione periodica poteva essere scomposta in una somma di infinite "opportune" funzioni o componenti sinusoidali (seno e coseno) dette armoniche. Da tale constatazione nasce dunque l'idea di scomporre funzioni complicate in una serie di funzioni, nota come serie di Fourier, rendendone l'analisi più semplice e vantaggiosa. Dal concetto matematico di serie di Fourier discende anche la nozione di trasformata di Fourier ed il relativo concetto associato di dominio della frequenza.

L'analisi armonica è la branca dell'analisi matematica che studia la rappresentazione delle funzioni o dei segnali come sovrapposizione di onde o fondamentali. Tali onde fondamentali sono chiamate "armoniche", da cui il nome "analisi armonica". Essa dunque indaga e generalizza la nozione di serie di Fourier e trasformata di Fourier. Nei precedenti due secoli è diventato un tema molto vasto con applicazioni in diverse aree come elaborazione numerica dei segnali, meccanica quantistica e neuroscienze. La classica trasformata di Fourier su R n {\displaystyle \mathbb {R} ^{n}} è ancora oggetto di ricerca, in particolare la trasformazione di Fourier di oggetti più generali come le distribuzioni temperate. Ad esempio, se si impongono alcuni requisiti a una distribuzione f {\displaystyle f} , si può cercare di tradurre questi requisiti in termini della trasformata di Fourier di f {\displaystyle f} . Il teorema di Paley-Wiener è un esempio di questo. Il teorema di Paley-Wiener implica immediatamente che se f {\displaystyle f} è una distribuzione non nulla di supporto compatto (questa definizione include le funzioni di supporto compatto), allora la sua trasformata di Fourier non ha mai supporto compatto. Questa è una forma molto elementare di principio di indeterminazione nell'ambito dell'analisi armonica. Le serie di Fourier possono essere agevolmente studiate nel contesto degli spazi di Hilbert, che offre un collegamento fra analisi armonica e analisi funzionale.