biblio toscana

La geometria euclidea è un sistema matematico attribuito al matematico alessandrino Euclide, che la descrisse nei suoi Elementi. La sua geometria consiste nell'assunzione di cinque semplici e intuitivi concetti, detti assiomi o postulati e, nella derivazione da detti assiomi, di altre proposizioni (teoremi) che non abbiano alcuna contraddizione con essi. Questa organizzazione della geometria permise l'introduzione della retta, del piano, della lunghezza e dell'area. Sebbene molte delle conclusioni di Euclide fossero già conosciute dai matematici, egli mostrò come queste potessero essere organizzate in una maniera deduttiva e con un sistema logico. Gli Elementi di Euclide incominciano con un'analisi della geometria piana, attualmente insegnata nelle scuole secondarie e utilizzata come primo approccio alle dimostrazioni matematiche, per poi passare alla geometria solida in tre dimensioni. Dopo Euclide sono nati particolari tipi di geometrie che non necessariamente rispettano i cinque postulati; tali geometrie sono definite non euclidee.

Euclide (in greco antico: Εὐκλείδης, Eukléidēs; IV secolo a.C. – III secolo a.C.) è stato un matematico e filosofo greco antico. Si occupò di vari ambiti, dall’ottica all’astronomia, dalla musica alla meccanica, oltre, ovviamente, alla matematica. Gli "Elementi", il suo lavoro più noto, è una delle più influenti opere di tutta la storia della matematica e fu uno dei principali testi per l'insegnamento della geometria dalla sua pubblicazione fino agli inizi del ‘900.

Gli Elementi (in greco antico: Στοιχεῖα, Stoichêia) di Euclide (matematico greco attivo intorno al 300 a.C.) sono la più importante opera matematica giuntaci dalla cultura greca antica. Contengono una prima formulazione di quella che oggi è conosciuta con il nome di geometria euclidea, rappresentando un quadro completo e definito dei principi della geometria noti al tempo. Oggi questi principi vengono formulati in modo più generale con i metodi dell'algebra lineare. La formulazione fatta da Euclide viene però ancora insegnata nelle scuole secondarie per fornire un primo esempio di sistema assiomatico e di dimostrazione rigorosa. L'opera consiste di 13 libri: i primi sei riguardanti la geometria piana, i successivi quattro i rapporti tra grandezze (in particolare il decimo libro riguarda la teoria degli incommensurabili) e gli ultimi tre la geometria solida. Alcune edizioni più antiche attribuiscono ad Euclide anche due ulteriori libri che la critica moderna assegna però ad altri autori. I diversi libri sono strutturati in definizioni e proposizioni (enunciati che potremmo anche chiamare teoremi). Delle proposizioni vengono fornite le dimostrazioni.

L'algoritmo di Euclide è un algoritmo per trovare il massimo comune divisore (indicato di seguito con MCD) tra due numeri interi. È uno degli algoritmi più antichi conosciuti, essendo presente negli Elementi di Euclide intorno al 300 a.C.; tuttavia, probabilmente l'algoritmo non è stato scoperto da Euclide, ma potrebbe essere stato conosciuto anche 200 anni prima. Certamente era conosciuto da Eudosso di Cnido intorno al 375 a.C.; Aristotele (intorno al 330 a.C.) ne ha fatto cenno ne I topici, 158b, 29-35. L'algoritmo non richiede la fattorizzazione dei due interi. Dati due numeri naturali a e b, si controlla se b è zero (questa prima fase rientra ovviamente nell'ambito di un uso moderno dell'algoritmo ed era ignorata da Euclide e dai suoi predecessori, che non conoscevano lo zero). Se lo è, a è il MCD. Se non lo è, si divide a / b e si assegna ad r il resto della divisione (operazione indicata con "a modulo b" più sotto). Se r = 0 allora si può terminare affermando che b è il MCD cercato, altrimenti occorre assegnare a' = b e b' = r e si ripete nuovamente la divisione. L'algoritmo può essere anche espresso in modo naturale utilizzando la ricorsione in coda. Tenendo nota dei quozienti ottenuti durante lo svolgimento dell'algoritmo, si possono determinare due interi p e q tali che ap + bq = MCD(a, b). Questo è noto con il nome di algoritmo di Euclide esteso. Questi algoritmi possono essere usati, oltre che con i numeri interi, in ogni contesto in cui è possibile eseguire la divisione col resto. Ad esempio, l'algoritmo funziona per i polinomi ad una indeterminata su un campo K, o polinomi omogenei a due indeterminate su un campo, o gli interi gaussiani. Un oggetto algebrico in cui è possibile eseguire la divisione col resto è chiamato anello euclideo. Euclide originariamente formulò il problema geometricamente, per trovare una "misura" comune per la lunghezza di due segmenti, e il suo algoritmo procedeva sottraendo ripetutamente il più corto dal più lungo. Questo procedimento è equivalente alla implementazione seguente, che è molto meno efficiente del metodo indicato sopra:

In geometria il punto è un concetto primitivo. Intuitivamente equivale ad un'entità adimensionale spaziale, per cui può essere considerato semplicemente come una posizione, cioè come una coordinata. In topologia ed analisi matematica, viene spesso chiamato punto un elemento qualunque di uno spazio topologico e, in particolare, di uno spazio funzionale.

In geometria, il primo teorema di Euclide è un teorema attinente al triangolo rettangolo che deriva, assieme al secondo, dalla proposizione 8 del VI libro degli Elementi di Euclide; nei testi scolastici può essere enunciato in due modi diversi a seconda della proprietà che si desidera sottolineare: mediante l'equiestensione tra figure: mediante relazioni tra segmenti:

In matematica, un numero primo (in breve anche primo) un numero intero positivo che abbia esattamente due divisori distinti. In modo equivalente si pu definire come un numero naturale maggiore di 1 che sia divisibile solamente per 1 e per s stesso; al contrario, un numero maggiore di 1 che abbia pi di due divisori detto composto. Ad esempio 2, 3 e 5 sono primi mentre 4 e 6 non lo sono perch sono divisibili rispettivamente anche per 2 e per 2 e 3. L'unico numero primo pari 2, in quanto tutti gli altri numeri pari sono divisibili per 2. La successione dei numeri primi comincia con 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 Quello di numero primo uno dei concetti basilari della teoria dei numeri, la parte della matematica che studia i numeri interi: l'importanza sta nella possibilit di costruire con essi, attraverso la moltiplicazione, tutti gli altri numeri interi, nonch l'unicit di tale fattorizzazione. I primi sono inoltre infiniti e la loro distribuzione tuttora oggetto di molte ricerche. I numeri primi sono oggetto di studio fin dall'antichit : i primi risultati risalgono infatti agli antichi Greci, e in particolare agli Elementi di Euclide, scritti attorno al 300 a.C. Ciononostante, numerose congetture che li riguardano non sono state ancora dimostrate; tra le pi note vi sono l'ipotesi di Riemann, la congettura di Goldbach e quella dei primi gemelli, indimostrate a pi di un secolo dalla loro formulazione. Essi sono rilevanti anche in molti altri ambiti della matematica pura, come ad esempio l'algebra o la geometria; recentemente hanno assunto un'importanza cruciale anche nella matematica applicata, e in particolare nella crittografia.

Con il termine moto browniano si fa riferimento al moto disordinato di particelle sufficientemente piccole (aventi diametro dell'ordine del micrometro) da essere sottoposte a una forza di gravità trascurabile, presenti in fluidi o sospensioni fluide o gassose (ad esempio il fumo), ed osservabile al microscopio. Il fenomeno fu scoperto agli inizi dell'Ottocento dal botanico scozzese Robert Brown, e modellizzato nel 1905 dal fisico teorico tedesco Albert Einstein.Il termine viene usato per indicare sia il fenomeno naturale sia la sua rappresentazione matematica, la quale può descrivere l'andamento temporale di una classe molto ampia di fenomeni casuali. Un'importante categoria di fenomeni rappresentabili con gli strumenti matematici del moto browniano è costituita dall'andamento dei mercati finanziari, come dimostrato sin dal 1900 dal matematico francese Louis Bachelier, nel suo lavoro Théorie de la spéculation.

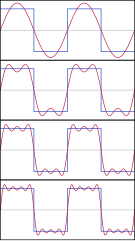
In analisi matematica, l'analisi di Fourier, nota anche come analisi armonica, è una branca di ricerca che ha preso avvio dalle ricerche di Jean Baptiste Joseph Fourier che, nei primi anni dell'Ottocento, riuscì a dimostrare matematicamente come una qualunque funzione periodica poteva essere scomposta in una somma di infinite "opportune" funzioni o componenti sinusoidali (seno e coseno) dette armoniche. Da tale constatazione nasce dunque l'idea di scomporre funzioni complicate in una serie di funzioni, nota come serie di Fourier, rendendone l'analisi più semplice e vantaggiosa. Dal concetto matematico di serie di Fourier discende anche la nozione di trasformata di Fourier ed il relativo concetto associato di dominio della frequenza.