biblio toscana

La logica matematica è il settore della matematica che studia i sistemi formali dal punto di vista del modo di codificare i concetti intuitivi della dimostrazione e di computazione come parte dei fondamenti della matematica. Essa si occupa delle parti della logica che possono essere modellate matematicamente. Altri termini utilizzati spesso nel passato sono logica simbolica (termine contrapposto a logica filosofica) e metamatematica, termine che ora si applica più specificamente a taluni aspetti della teoria della dimostrazione.

Principia Mathematica è un'opera sui fondamenti logici della matematica scritta da Alfred North Whitehead e Bertrand Russell. L'opera è divisa in tre volumi pubblicati nel 1910, 1912, e 1913 dalla Cambridge University Press. Nel 1927 è apparsa una seconda edizione con una nuova Introduzione e una nuova Appendice C. Una versione ridotta è apparsa nel 1962 col titolo Principia Mathematica to *56. L'Introduzione è stata tradotta in italiano da Paolo Parrini per i tipi de La Nuova Italia con il titolo Introduzione ai «Principia mathematica» (1977).

I principi della dinamica sono le leggi fisiche su cui si fonda la dinamica newtoniana, che descrive le relazioni tra il moto di un corpo e gli enti che lo modificano. Sono validi in sistemi di riferimento inerziali e descrivono accuratamente il comportamento dei corpi che si muovono a velocità molto minori della velocità della luce, condizione in cui sono assimilabili con buona approssimazione ai principi più generali della relatività ristretta. Sono anche chiamati principi di Newton perché furono enunciati come assiomi da Isaac Newton nel suo trattato Philosophiae Naturalis Principia Mathematica, pur essendo il frutto di una lunga evoluzione da parte di numerosi scienziati che ne ha preceduto e seguito la pubblicazione; in particolare sono stati riformulati storicamente in vari modi, tra cui la formulazione lagrangiana e la formulazione hamiltoniana.

Pietro Catena (Venezia, 1501 – Padova, 1576) è stato un astronomo, filosofo, matematico, teologo e religioso italiano della Repubblica di Venezia. Fu un precursore della rivoluzione scientifica rinascimentale e indagò i rapporti tra matematica, logica e filosofia, occupando la stessa cattedra in seguito occupata da Galileo.

Il pensiero di Leibniz s'inserisce nel dibattito metafisico sulla sostanza, aperto da Cartesio e giunto alla sua conclusione con le filosofie di Spinoza e di Locke, alle quali Leibniz si opporrà.

Mathematica è un ambiente di calcolo simbolico e numerico multipiattaforma, ideato da Stephen Wolfram e successivamente sviluppato da un team di matematici e programmatori. Mathematica usa un potente linguaggio di programmazione interpretato, chiamato linguaggio Wolfram. Wolfram e il suo gruppo iniziarono a lavorare al programma nel 1986 e pubblicarono la prima versione nel 1988. La versione corrente è la 12.1, uscita il 18 marzo 2020. Il sistema Mathematica è disponibile per le piattaforme Windows, MacOS e Linux.

La matematica (dal greco μάθημα (máthema), traducibile con i termini "scienza", "conoscenza" o "apprendimento"; μαθηματικός (mathematikós) significa "incline ad apprendere") è la disciplina che studia le quantità (i numeri), lo spazio, le strutture e i calcoli.Per l'origine del termine occorre andare al vocabolo egizio maat, nella cui composizione appare il simbolo del cubito, strumento di misura lineare, un primo accostamento al concetto matematico. Simbolo geometrico di questo ordine è un rettangolo, da cui sorge la testa piumata della dea egizia Maat, personificazione dei concetti di ordine, verità e giustizia. Figlia di Ra, unico Uno, creatore di ogni cosa, la sua potenza demiurgica è limitata e ordinata da leggi naturali e matematiche. All'inizio del papiro di Rhind si trova questa affermazione: "Il calcolo accurato è la porta d'accesso alla conoscenza di tutte le cose e agli oscuri misteri". Il termine maat riappare in copto, in babilonese e in greco. In greco la radice ma, math, met entra nella composizione di vocaboli contenenti le idee di ragione, disciplina, scienza, istruzione, giusta misura, e in latino il termine materia indica ciò che può essere misurato. Col termine matematica di solito si designa la disciplina (e il relativo corpo di conoscenze) che studia problemi concernenti quantità, estensioni e figure spaziali, movimenti di corpi, e tutte le strutture che permettono di trattare questi aspetti in modo generale. La matematica fa largo uso degli strumenti della logica e sviluppa le proprie conoscenze nel quadro di sistemi ipotetico-deduttivi che, a partire da definizioni rigorose e da assiomi riguardanti proprietà degli oggetti definiti (risultati da un procedimento di astrazione, come triangoli, funzioni, vettori ecc.), raggiunge nuove certezze, per mezzo delle dimostrazioni, attorno a proprietà meno intuitive degli oggetti stessi (espresse dai teoremi). La potenza e la generalità dei risultati della matematica le ha reso l'appellativo di regina delle scienze: ogni disciplina scientifica o tecnica, dalla fisica all'ingegneria, dall'economia all'informatica, fa largo uso degli strumenti di analisi, di calcolo e di modellazione offerti dalla matematica.

La filosofia della matematica è la branca della filosofia della scienza che cerca di dare risposta a domande quali: "perché la matematica è utile nella descrizione della natura?", "in quale senso, qualora se ne trovi uno, le entità matematiche (in particolare i numeri) esistono?" "perché e in che modo gli enunciati matematici sono veri?". In questo articolo sono presentati i vari approcci che vengono seguiti per rispondere a questioni come le precedenti. È utile precisare che tre sono i problemi della filosofia della matematica: Un problema ontologico: risponde alla domanda "Esistono i numeri?"; Un problema metafisico: risponde alla domanda "Che cosa sono i numeri?"; Un problema epistemologico: "Come facciamo ad accedere epistemicamente alle verità della matematica o, meglio, come possiamo sapere che ciò che ci dice la matematica è vero?";Questi sono i problemi che la maggior parte dei filosofi, oggigiorno, ritengano debbano essere risolti da una buona filosofia della matematica.

In matematica si chiamano postulati o assiomi tutti e soli gli enunciati che, pur non essendo stati dimostrati, sono considerati veri. Generalmente forniscono il punto di partenza per delineare un quadro teorico come può essere quello della teoria degli insiemi, della geometria, dell'aritmetica, della teoria dei gruppi o nel calcolo delle probabilità. Nella logica matematica l'idea di assioma e dimostrazione viene completamente formalizzata. Gli assiomi di una teoria proposizionale o di una teoria del primo ordine sono un ben definito insieme di formule che possono essere usate nella teoria per costruire dimostrazioni formali. In questo ambito si fa una netta distinzione tra le due nozioni di assioma logico e assioma non-logico.

Gottfried Wilhelm von Leibniz (pronuncia tedesca [ˈlaɪ̯pnɪʦ]; latinizzato in Leibnitius, e talvolta italianizzato in Leibnizio; tedesco e francese desueto Leibnitz; Lipsia, 1º luglio 1646 – Hannover, 14 novembre 1716) è stato un filosofo, matematico, scienziato, logico, teologo, linguista, glottoteta, diplomatico, giurista, storico, magistrato tedesco. E' uno dei massimi esponenti del pensiero occidentale, nonché una delle poche figure di "genio universale"; la sua applicazione intellettuale a pressoché tutte le discipline del sapere ne rende l'opera vastissima e studiata ancor oggi trasversalmente. A lui, assieme a Isaac Newton, vengono generalmente attribuiti l'introduzione e i primi sviluppi del calcolo infinitesimale, in particolare il concetto di integrale, per il quale si usano ancora oggi molte sue notazioni. A Leibniz si devono i termini "funzione", che egli usò per individuare le proprietà di una curva, tra cui l'andamento, la pendenza, la corda, la perpendicolare in un punto, e "dinamica".Considerato il precursore dell'informatica, della neuroinformatica e del calcolo automatico, fu inventore di una calcolatrice meccanica detta Macchina di Leibniz; inoltre alcuni ambiti della sua filosofia aprirono numerosi spiragli sulla dimensione dell'inconscio che solo nel XX secolo, con Sigmund Freud si tenterà di esplorare.

Il circolo di Vienna (in tedesco Wiener Kreis), fu un circolo filosofico e culturale, organizzato da Moritz Schlick nel 1922 e animato da numerosi filosofi e scienziati del tempo. L'approccio filosofico del Circolo, noto come positivismo logico (o neopositivismo) o anche fisicalismo, si diffuse nel resto dell'Europa e nei Paesi di lingua inglese. Le riunioni del circolo si tennero ogni settimana con regolarità fino all'avvento del nazismo. La morte violenta di Schlick (1936), assassinato sulle scale dell'università di Vienna da un fanatico nazista, e la fuga dalla città dei suoi membri per evitare le persecuzioni politiche e razziali del nuovo regime, ne segnarono la fine. Alle sedute del circolo parteciparono con assiduità: Rudolf Carnap, Otto Neurath, Philipp Frank, Friedrich Waismann (assistente di Schlick), il matematico Hans Hahn, Gustav Bergmann, Carl Menger, Herbert Feigl, Viktor Kraft, Ludwig von Bertalanffy. Ne furono ospiti occasionali Hans Reichenbach, Kurt Gödel, Carl Hempel, Alfred Tarski, Willard Van Orman Quine, Alfred Julius Ayer, Arne Næss. Ludwig Wittgenstein e Karl Popper non furono mai presenti alle riunioni del circolo anche se, negli stessi anni, intrattennero rapporti con i suoi membri. Il Circolo organizzò conferenze internazionali su temi scientifici e filosofici; la prima fu tenuta a Praga nel 1929 ove fu distribuito il manifesto per una Wissenschaftliche Weltauffassung (concezione scientifica del mondo), composto soprattutto da Neurath, Carnap e Hahn, dedicato a Moritz Schlick.

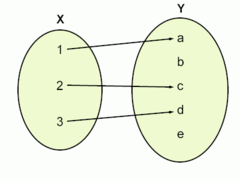
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).

Questo è un glossario della simbologia matematica costituito da tabelle dedicate ai simboli utilizzati in matematica.

La logica (dal greco λόγος, logos, ovvero "parola", "pensiero", "idea", "argomento", "ragione", da cui poi λογική, logiké) è lo studio del ragionamento e dell'argomentazione, rivolto in particolare a definire la correttezza dei procedimenti inferenziali del pensiero.

In matematica il concetto di infinito (simbolo ∞ {\displaystyle \infty } ) ha molti significati, in correlazione con la nozione di limite, sia in analisi classica sia in analisi non standard. Nozioni di infinito sono usate in teoria degli insiemi e in geometria proiettiva.

La matematica, nel corso della sua storia, è diventata una materia estremamente diversificata, di conseguenza si è reso necessario categorizzarne le aree. Nel frattempo sono sorti un certo numero di schemi di classificazione, e, anche se condividono alcune somiglianze, in essi sono presenti differenze dovute in parte ai diversi scopi per cui sono stati creati. Inoltre, dal momento che la matematica si evolve, questi schemi di classificazione devono a loro volta evolversi, anche a causa della scoperta di nuove aree o di collegamenti appena individuati tra quelle preesistenti. La classificazione inoltre è resa più difficile da parte di alcuni settori, spesso i più attivi, che si situano ai confini delle diverse aree. La matematica è divisa tradizionalmente in matematica pura, studiata per il suo interesse intrinseco, e matematica applicata, la matematica applicabile direttamente a problemi del mondo reale. Questa divisione non è sempre chiara e molti argomenti sono stati sviluppati nello studio della matematica pura per trovare in seguito inaspettate applicazioni. Più recentemente sono emerse divisioni di massima, come la matematica discreta e matematica computazionale.

Sir Isaac Newton (citato anche come Isacco Newton) (Woolsthorpe-by-Colsterworth, 25 dicembre 1642 – Londra, 20 marzo 1726) è stato un matematico, fisico, filosofo naturale, astronomo, teologo, storico e alchimista inglese, considerato uno dei più grandi scienziati di tutti i tempi, ricoprendo anche il ruolo di direttore della zecca inglese e quello di Presidente della Royal Society. Noto soprattutto per il suo contributo alla meccanica classica, contribuì in maniera fondamentale a più di una branca del sapere, occupando una posizione di grande rilievo nella storia della scienza e della cultura in generale, con il suo nome che è associato a una grande quantità di leggi e teorie ancora oggi insegnate: si parla così di dinamica newtoniana, di leggi newtoniane del moto, di legge di gravitazione universale; più in generale ci si riferisce al newtonianesimo come a una concezione del mondo che ha influenzato la cultura europea per tutto il Seicento. Attratto dalla filosofia naturale, ben presto cominciò a leggere le opere di Cartesio, in particolare La geometria del 1637, in cui le curve sono rappresentate per mezzo di equazioni; negli anni in cui era studente a Cambridge alla cattedra presiedevano due figure di grande rilievo, Isaac Barrow e Henry More, che esercitarono una forte influenza sul ragazzo; negli anni seguenti, costruì le sue scoperte matematiche e sperimentali facendo riferimento a un gruppo ristretto di testi: pubblicò i Philosophiae Naturalis Principia Mathematica nel 1687, opera nella quale descrisse la legge di gravitazione universale e, attraverso le sue leggi del moto, costruì le regole fondamentali per la meccanica classica, condividendo con Gottfried Wilhelm Leibniz la paternità dello sviluppo del calcolo differenziale o infinitesimale. Contribuì alla rivoluzione scientifica e al progresso della teoria eliocentrica: a lui si deve la sistematizzazione matematica delle leggi di Keplero sul movimento dei pianeti; oltre a dedurle matematicamente dalla soluzione del problema della dinamica applicata alla forza di gravità (problema dei due corpi) ovvero dalle omonime equazioni di Newton, egli generalizzò queste leggi intuendo che le orbite (come quelle delle comete) potevano essere non solo ellittiche, ma anche iperboliche e paraboliche, dimostrando anche che le medesime leggi della natura governano il movimento della Terra e degli altri corpi celesti. Fu il primo a dimostrare che la luce bianca è composta dalla somma (in frequenza) di tutti gli altri colori, avanzando l'ipotesi che la luce fosse composta da particelle, dando così vita alla teoria corpuscolare della luce, in contrapposizione alla teoria ondulatoria della luce patrocinata dall'astronomo olandese Christiaan Huygens e dall'inglese Thomas Young e corroborata alla fine dell'Ottocento dai lavori di Maxwell e Hertz; la tesi di Newton trovò invece conferme, circa due secoli dopo, con l'introduzione del quanto d'azione da parte di Max Planck (1900) e con l'articolo di Albert Einstein (1905) sull'interpretazione dell'effetto fotoelettrico a partire dal quanto di radiazione elettromagnetica, poi denominato fotone; queste due interpretazioni coesisteranno nell'ambito della meccanica quantistica, come previsto dal dualismo onda-particella.

Un matematico è una persona che effettua studi, ricerche e sperimentazioni riguardanti problemi della matematica. Alcuni scienziati di altri campi di ricerca possono essere considerati matematici se la loro ricerca offre nuove idee matematiche; un esempio notevole è Edward Witten. Al contrario, alcuni matematici possono studiare problemi matematici relativi ad altri settori della ricerca scientifica e tecnologica (es. fisica matematica), queste persone sono conosciute come matematici applicati.

Introduzione alla filosofia matematica è un'opera del filosofo gallese Bertrand Russell. Si propone di esporre i più basilari concetti che stanno alla base della matematica. Fu scritta durante il periodo di carcerazione scontato dall'autore per la sua partecipazione al movimento pacifista inglese durante la prima guerra mondiale. La trattazione è operata in una forma adatta ai non addetti ai lavori, evitando l'uso della simbologia più propria della materia e rinviando a Principia Mathematica per l'approfondimento degli aspetti tecnici più complessi. Il libro si sviluppa attraverso l'analisi di diversi argomenti, a ciascuno dei quali è dedicato un capitolo; tale percorso arriva in conclusione a mostrare l'arbitrarietà che secondo l'autore è presente in ogni tentativo di marcare un confine tra logica e matematica. L'indice dei capitoli: La serie dei numeri naturali La definizione di numero Il finito e l'induzione matematica La definizione di ordine Tipi di relazioni Similitudine tra relazioni I numeri razionali, reali e complessi Numeri cardinali infiniti Serie e ordinali infiniti Limiti e continuità Limiti e continuità delle funzioni Le selezioni e l'assioma moltiplicativo L'assioma dell'infinito e i tipi logici L'incompatibilità e l'assioma della deduzione Le funzioni proposizionali Le descrizioni Le classi Matematica e logica