biblio toscana

L'aritmetica (dal greco ἀριθμός = numero) è la più antica branca della matematica, quella che studia le proprietà elementari delle operazioni aritmetiche sui numeri, specialmente i numeri interi. È praticata quotidianamente da tutti per scopi molto semplici, come contare oggetti, valutare costi, stabilire distanze; viene utilizzata anche per scopi avanzati, ad esempio in complessi calcoli finanziari o nella tecnologia delle comunicazioni (crittografia). I matematici talvolta usano il termine aritmetica per indicare la teoria dei numeri; questa disciplina però tratta problemi più avanzati e specifici rispetto all'aritmetica elementare e non viene presa in considerazione nel presente articolo.

L'aritmetica modulare (a volte detta aritmetica dell'orologio poiché su questo principio si basa il calcolo delle ore a cicli di 12 o 24) rappresenta un importante ramo della matematica. Trova applicazioni nella crittografia, nella teoria dei numeri (in particolare nella ricerca dei numeri primi) ed è alla base di molte delle più comuni operazioni aritmetiche e algebriche. Si tratta di un sistema di aritmetica degli interi, in cui i numeri "si avvolgono su loro stessi" ogni volta che raggiungono i multipli di un determinato numero n, detto modulo. L'aritmetica modulare e la notazione usuale delle congruenze vennero formalmente introdotte da Carl Friedrich Gauss nel suo trattato Disquisitiones Arithmeticae, pubblicato nel 1801.

La scuola secondaria di secondo grado (comunemente detta scuola superiore) è, nell'ordinamento scolastico italiano, il secondo ciclo di studi dell'obbligo. Lo studente vi accede dopo aver conseguito la licenza media, con possibilità di scegliere a quale istituto iscriversi.Gli istituti superiori hanno durata quinquennale, solitamente suddivisa in biennio comune e triennio specialistico; lo studente compie tale ciclo di studi generalmente dall'età di 14 anni fino a 20. Al termine del percorso scolastico viene sostenuto l'esame di maturità, con il rilascio del diploma; il titolo consente l'iscrizione all'università.

Un'operazione aritmetica, in matematica, è un'operazione binaria tra numeri: partendo da almeno due numeri, detti «operandi», si ottiene un unico risultato (che è anch'esso un numero), dipendente dal tipo di operazione od «operatore» utilizzato. Ogni operazione è identificata da un simbolo. Oltre all'operazione diretta esiste l'operazione inversa, che permette di risalire dal risultato ai numeri iniziali.

La logica matematica è il settore della matematica che studia i sistemi formali dal punto di vista del modo di codificare i concetti intuitivi della dimostrazione e di computazione come parte dei fondamenti della matematica. Essa si occupa delle parti della logica che possono essere modellate matematicamente. Altri termini utilizzati spesso nel passato sono logica simbolica (termine contrapposto a logica filosofica) e metamatematica, termine che ora si applica più specificamente a taluni aspetti della teoria della dimostrazione.

Sir Isaac Newton (citato anche come Isacco Newton) (Woolsthorpe-by-Colsterworth, 25 dicembre 1642 – Londra, 20 marzo 1726) è stato un matematico, fisico, filosofo naturale, astronomo, teologo, storico e alchimista inglese, considerato uno dei più grandi scienziati di tutti i tempi, ricoprendo anche il ruolo di direttore della zecca inglese e quello di Presidente della Royal Society. Noto soprattutto per il suo contributo alla meccanica classica, contribuì in maniera fondamentale a più di una branca del sapere, occupando una posizione di grande rilievo nella storia della scienza e della cultura in generale, con il suo nome che è associato a una grande quantità di leggi e teorie ancora oggi insegnate: si parla così di dinamica newtoniana, di leggi newtoniane del moto, di legge di gravitazione universale; più in generale ci si riferisce al newtonianesimo come a una concezione del mondo che ha influenzato la cultura europea per tutto il Seicento. Attratto dalla filosofia naturale, ben presto cominciò a leggere le opere di Cartesio, in particolare La geometria del 1637, in cui le curve sono rappresentate per mezzo di equazioni; negli anni in cui era studente a Cambridge alla cattedra presiedevano due figure di grande rilievo, Isaac Barrow e Henry More, che esercitarono una forte influenza sul ragazzo; negli anni seguenti, costruì le sue scoperte matematiche e sperimentali facendo riferimento a un gruppo ristretto di testi: pubblicò i Philosophiae Naturalis Principia Mathematica nel 1687, opera nella quale descrisse la legge di gravitazione universale e, attraverso le sue leggi del moto, costruì le regole fondamentali per la meccanica classica, condividendo con Gottfried Wilhelm Leibniz la paternità dello sviluppo del calcolo differenziale o infinitesimale. Contribuì alla rivoluzione scientifica e al progresso della teoria eliocentrica: a lui si deve la sistematizzazione matematica delle leggi di Keplero sul movimento dei pianeti; oltre a dedurle matematicamente dalla soluzione del problema della dinamica applicata alla forza di gravità (problema dei due corpi) ovvero dalle omonime equazioni di Newton, egli generalizzò queste leggi intuendo che le orbite (come quelle delle comete) potevano essere non solo ellittiche, ma anche iperboliche e paraboliche, dimostrando anche che le medesime leggi della natura governano il movimento della Terra e degli altri corpi celesti. Fu il primo a dimostrare che la luce bianca è composta dalla somma (in frequenza) di tutti gli altri colori, avanzando l'ipotesi che la luce fosse composta da particelle, dando così vita alla teoria corpuscolare della luce, in contrapposizione alla teoria ondulatoria della luce patrocinata dall'astronomo olandese Christiaan Huygens e dall'inglese Thomas Young e corroborata alla fine dell'Ottocento dai lavori di Maxwell e Hertz; la tesi di Newton trovò invece conferme, circa due secoli dopo, con l'introduzione del quanto d'azione da parte di Max Planck (1900) e con l'articolo di Albert Einstein (1905) sull'interpretazione dell'effetto fotoelettrico a partire dal quanto di radiazione elettromagnetica, poi denominato fotone; queste due interpretazioni coesisteranno nell'ambito della meccanica quantistica, come previsto dal dualismo onda-particella.

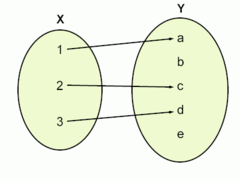
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).

L'Europa orientale è la regione orientale dell'Europa e può indicare: la regione compresa tra l'Europa orientale e la Russia europea. Questa è la definizione contemporanea successiva alla dissoluzione del patto di Varsavia; la regione delimitata a est dagli Urali e a ovest dai confini dei tradizionali membri dell'Unione europea.

La topologia (dal greco τόπος, tópos, "luogo", e λόγος, lógos, "studio", col significato quindi di "studio dei luoghi'") è una branca della geometria che studia le proprietà delle figure, e in generale degli oggetti matematici, che non cambiano quando viene effettuata una deformazione senza "strappi", "sovrapposizioni" o "incollature". È una delle più importanti branche della matematica moderna. Concetti fondamentali come convergenza, limite, continuità, connessione o compattezza trovano nella topologia la loro migliore formalizzazione. Si basa essenzialmente sui concetti di spazio topologico, funzione continua e omeomorfismo. Col termine topologia si indica anche la collezione di aperti che definisce uno spazio topologico. Per esempio un cubo e una sfera sono oggetti topologicamente equivalenti (cioè omeomorfi), perché possono essere deformati l'uno nell'altro senza ricorrere ad alcuna incollatura, strappo o sovrapposizione; una sfera e un toro invece non lo sono, perché il toro contiene un "buco" che non può essere eliminato da una deformazione.

La geometria euclidea è un sistema matematico attribuito al matematico alessandrino Euclide, che la descrisse nei suoi Elementi. La sua geometria consiste nell'assunzione di cinque semplici e intuitivi concetti, detti assiomi o postulati e, nella derivazione da detti assiomi, di altre proposizioni (teoremi) che non abbiano alcuna contraddizione con essi. Questa organizzazione della geometria permise l'introduzione della retta, del piano, della lunghezza e dell'area. Sebbene molte delle conclusioni di Euclide fossero già conosciute dai matematici, egli mostrò come queste potessero essere organizzate in una maniera deduttiva e con un sistema logico. Gli Elementi di Euclide incominciano con un'analisi della geometria piana, attualmente insegnata nelle scuole secondarie e utilizzata come primo approccio alle dimostrazioni matematiche, per poi passare alla geometria solida in tre dimensioni. Dopo Euclide sono nati particolari tipi di geometrie che non necessariamente rispettano i cinque postulati; tali geometrie sono definite non euclidee.

Tullio Levi-Civita (Padova, 29 marzo 1873 – Roma, 29 dicembre 1941) è stato un matematico e fisico italiano.

Benedetto Croce (Pescasseroli, 25 febbraio 1866 – Napoli, 20 novembre 1952) è stato un filosofo, storico, politico, critico letterario e scrittore italiano, principale ideologo del liberalismo novecentesco italiano ed esponente del neoidealismo. Presentò il suo idealismo come «storicismo assoluto», giacché «la filosofia non può essere altro che "filosofia dello spirito" [...] e la filosofia dello spirito non può essere altro che "pensiero storico"», ossia «pensiero che ha come contenuto la storia», che rifugge ogni metafisica, la quale è «filosofia di una realtà immutabile trascendente lo spirito». In funzione anti-positivistica, nella filosofia crociana, la scienza diventa la misuratrice della realtà, sottomessa alla filosofia, che invece comprende e spiega il reale. Con Giovanni Gentile – dal quale lo separarono la concezione filosofica e la posizione politica nei confronti del fascismo dopo il delitto Matteotti – è considerato tra i maggiori protagonisti della cultura italiana ed europea della prima metà del XX secolo, in particolare dell'idealismo. La dottrina crociana improntata alla storiografia ebbe grande influenza politica sulla cultura italiana; Croce, in particolare, con la sua "religione della libertà, è ricordato come guida morale dell'antifascismo ", tanto che fu anche proposto come Presidente della Repubblica italiana. Fu tra i fondatori del ricostituito Partito Liberale Italiano, assieme a Luigi Einaudi.Alcune riserve sulla sua estetica, come anche sulla critica letteraria (in particolare sulla sua definizione di «poesia») e sulla superiorità attribuita da Croce alla filosofia rispetto alle scienze nell'ambito della logica, sono state, tuttavia, espresse in tempi successivi.D'altra parte, il pensiero di Croce, specialmente quello politico, ha goduto di apprezzamenti più recenti e di una "riscoperta" anche al di fuori dell'Italia, in Europa e nel mondo anglosassone (specialmente gli Stati Uniti d'America), dov'è riconosciuto, al pari di pensatori come Karl Popper, come uno dei più eminenti teorici del liberalismo europeo e un autorevole oppositore di ogni totalitarismo. Il liberalismo politico crociano distinto dal liberismo economico fu causa di disaccordo con un altro importante esponente del liberalismo italiano come Luigi Einaudi.

Giovanni Antonio Cybei (Carrara, 3 febbraio 1706 – Carrara, 7 settembre 1784) è stato uno scultore e religioso italiano, nobile modenese, primo direttore dell'Accademia di Belle Arti di Carrara.

Il Dialogo sopra i due massimi sistemi del mondo è un celeberrimo trattato di Galileo Galilei, scritto sotto forma dialogica negli anni tra il 1624 e il 1630 e pubblicato nel 1632. L'opera, strutturata nel dialogo fra tre personaggi: Simplicio (che riprende il nome dell'antico filosofo del VI secolo Simplicio di Cilicia), Sagredo e Filippo Salviati, ebbe da subito un enorme successo, ma la Chiesa, che dapprima ne aveva concesso l'imprimatur, mutò radicalmente la sua posizione, inserendola nell'Indice dei libri proibiti nel 1633. Il Dialogo si presenta, nonostante la lettera nicodemica iniziale, come una confutazione del sistema tolemaico-aristotelico a favore di un sistema copernicano, benché le teorie moderne rivelino l'inesattezza della dimostrazione galileiana sulle maree.Si pone però come un importante scritto filosofico all'interno di quella che sarà l'imminente rivoluzione scientifica, conciliando linguaggio e semplicità divulgative. Il nuovo metodo scientifico (o appunto metodo galileiano) si muoverà da questa sua pubblicazione, in particolar modo verrà esplicata la teoria della conoscenza di Galileo. Oltre che un trattato scientifico-astronomico infatti si presenta come una grande opera filosofica.

In matematica si chiamano postulati o assiomi tutti e soli gli enunciati che, pur non essendo stati dimostrati, sono considerati veri. Generalmente forniscono il punto di partenza per delineare un quadro teorico come può essere quello della teoria degli insiemi, della geometria, dell'aritmetica, della teoria dei gruppi o nel calcolo delle probabilità. Nella logica matematica l'idea di assioma e dimostrazione viene completamente formalizzata. Gli assiomi di una teoria proposizionale o di una teoria del primo ordine sono un ben definito insieme di formule che possono essere usate nella teoria per costruire dimostrazioni formali. In questo ambito si fa una netta distinzione tra le due nozioni di assioma logico e assioma non-logico.

Guido Castelnuovo (Venezia, 14 agosto 1865 – Roma, 27 aprile 1952) è stato un matematico, statistico e accademico italiano, principalmente conosciuto per i suoi fondamentali contributi alla geometria algebrica.

Un modello matematico è una rappresentazione quantitativa di un fenomeno naturale. Come tutti gli altri modelli usati nella scienza, il suo scopo è quello di rappresentare il più incisivamente possibile un determinato oggetto, un fenomeno reale o un insieme di fenomeni (modello matematico di un sistema fisico, sistema chimico o sistema biologico). Spesso il modello è una rappresentazione della realtà non perfetta, ma comunque fedele, ovvero significativa all'analisi o prognosi che si vuole condurre. Tutti i settori della scienza, ma non solo, fanno largo uso di modelli matematici per modellizzare determinati aspetti del mondo. Gli strumenti matematici usati possono essere i più disparati, dalla combinatoria al calcolo infinitesimale: per molti fenomeni per esempio una descrizione molto sintetica e intuitiva è formulabile immediatamente tramite delle equazioni differenziali. In particolare il modello matematico consente di operare delle prognosi future su un sistema ed è ciò che distingue la scienza quantitativa dalla scienza qualitativa.

L'Europa (/euˈrɔpa/) è una regione geografica del mondo, comunemente considerata un continente in base a fattori storico-culturali e geopolitici, l'unico situato interamente nell'emisfero settentrionale. Costituisce l'estremità occidentale del supercontinente Eurasia, o anche una delle tre parti del supercontinente Eurafrasia. È stata la culla della civiltà occidentale, assieme al Medio Oriente. La storia e la cultura europea hanno influenzato notevolmente quelle degli altri continenti, verso i quali, a partire dal XVI secolo, sono state frequenti e massicce le migrazioni, specialmente in America e in Oceania, dove gli europei sono ora in maggioranza rispetto alle popolazioni locali; varie forme di colonialismo e di imperialismo europeo hanno influenzato profondamente la Storia degli ultimi secoli.

Questo è un glossario della simbologia matematica costituito da tabelle dedicate ai simboli utilizzati in matematica.

Europa&Italia è un cortometraggio del 1999 diretto da Bruno Bozzetto. Il comportamento degli italiani a confronto con quello del resto degli europei.

In geometria, il secondo teorema di Euclide è un teorema concernente il triangolo rettangolo che deriva, assieme al primo, dalla proposizione 8 del VI libro degli Elementi di Euclide.

La Pontificia accademia delle scienze (in latino: Pontificia Academia Scientiarum) è un'accademia pontificia nata con lo scopo di promuovere il progresso della matematica, della fisica e delle scienze naturali e lo studio dei relativi problemi epistemologici. È erede dell'originaria Accademia dei Lincei, fondata a Roma nell'anno 1603 dal principe Federico Cesi; l'attuale istituzione è stata rifondata con questo nome nell'anno 1936 da papa Pio XI. Ha sede nel casino di Pio IV, nei giardini vaticani.

Pietro Catena (Venezia, 1501 – Padova, 1576) è stato un astronomo, filosofo, matematico, teologo e religioso italiano della Repubblica di Venezia. Fu un precursore della rivoluzione scientifica rinascimentale e indagò i rapporti tra matematica, logica e filosofia, occupando la stessa cattedra in seguito occupata da Galileo.

Il circolo di Vienna (in tedesco Wiener Kreis), fu un circolo filosofico e culturale, organizzato da Moritz Schlick nel 1922 e animato da numerosi filosofi e scienziati del tempo. L'approccio filosofico del Circolo, noto come positivismo logico (o neopositivismo) o anche fisicalismo, si diffuse nel resto dell'Europa e nei Paesi di lingua inglese. Le riunioni del circolo si tennero ogni settimana con regolarità fino all'avvento del nazismo. La morte violenta di Schlick (1936), assassinato sulle scale dell'università di Vienna da un fanatico nazista, e la fuga dalla città dei suoi membri per evitare le persecuzioni politiche e razziali del nuovo regime, ne segnarono la fine. Alle sedute del circolo parteciparono con assiduità: Rudolf Carnap, Otto Neurath, Philipp Frank, Friedrich Waismann (assistente di Schlick), il matematico Hans Hahn, Gustav Bergmann, Carl Menger, Herbert Feigl, Viktor Kraft, Ludwig von Bertalanffy. Ne furono ospiti occasionali Hans Reichenbach, Kurt Gödel, Carl Hempel, Alfred Tarski, Willard Van Orman Quine, Alfred Julius Ayer, Arne Næss. Ludwig Wittgenstein e Karl Popper non furono mai presenti alle riunioni del circolo anche se, negli stessi anni, intrattennero rapporti con i suoi membri. Il Circolo organizzò conferenze internazionali su temi scientifici e filosofici; la prima fu tenuta a Praga nel 1929 ove fu distribuito il manifesto per una Wissenschaftliche Weltauffassung (concezione scientifica del mondo), composto soprattutto da Neurath, Carnap e Hahn, dedicato a Moritz Schlick.

Gottfried Wilhelm von Leibniz (pronuncia tedesca [ˈlaɪ̯pnɪʦ]; latinizzato in Leibnitius, e talvolta italianizzato in Leibnizio; tedesco e francese desueto Leibnitz; Lipsia, 1º luglio 1646 – Hannover, 14 novembre 1716) è stato un filosofo, matematico, scienziato, logico, teologo, linguista, glottoteta, diplomatico, giurista, storico, magistrato tedesco. E' uno dei massimi esponenti del pensiero occidentale, nonché una delle poche figure di "genio universale"; la sua applicazione intellettuale a pressoché tutte le discipline del sapere ne rende l'opera vastissima e studiata ancor oggi trasversalmente. A lui, assieme a Isaac Newton, vengono generalmente attribuiti l'introduzione e i primi sviluppi del calcolo infinitesimale, in particolare il concetto di integrale, per il quale si usano ancora oggi molte sue notazioni. A Leibniz si devono i termini "funzione", che egli usò per individuare le proprietà di una curva, tra cui l'andamento, la pendenza, la corda, la perpendicolare in un punto, e "dinamica".Considerato il precursore dell'informatica, della neuroinformatica e del calcolo automatico, fu inventore di una calcolatrice meccanica detta Macchina di Leibniz; inoltre alcuni ambiti della sua filosofia aprirono numerosi spiragli sulla dimensione dell'inconscio che solo nel XX secolo, con Sigmund Freud si tenterà di esplorare.

Il Liber abbaci, noto anche come Liber abaci, è un trattato di argomento matematico. Scritto in latino medievale nel 1202 dal matematico pisano Leonardo Fibonacci, che nel 1228 ne pubblicò una seconda stesura, ha svolto un ruolo fondamentale nella storia della matematica occidentale ed è ritenuto uno dei libri più importanti e fecondi del Medioevo.Il Liber abbaci è un ponderoso trattato di aritmetica e algebra con il quale, all'inizio del XIII secolo, Fibonacci ha introdotto in Europa il sistema numerico decimale indo-arabico e i principali metodi di calcolo ad esso relativi. Il libro non tratta l'utilizzo dell'abaco, sicché il suo titolo può essere tradotto in Libro del calcolo: dato che abaco per i greci, i romani e i maestri d'abaco dei secoli precedenti era uno strumento di calcolo, secondo alcuni studiosi il titolo non sarebbe autoriale, per quanto non vi siano dubbi che il Fibonacci abbia in effetti riservato questa denominazione all'aritmetica-algebra applicativa in genere. Su questo trattato, per oltre tre secoli, si formeranno maestri e allievi della scuola toscana. L'equilibrio fra teoria e pratica era di fatto raggiunto. Fibonacci dice: "Ho dimostrato con prove certe quasi tutto quello che ho trattato". Quando Fibonacci scrisse il trattato, in Europa gli scritti di matematica avanzata erano quasi del tutto inesistenti, a parte le traduzioni delle opere classiche (gli Elementi di Euclide, per esempio), che però erano ancora molto poco diffuse, e i cosiddetti Algorismi, scritti di aritmetica latina che prendevano il nome dal matematico al-Khwarizmi. Fibonacci compì un'operazione unica, diversa da quelle degli Arabi, se non per l'originalità certo per la mole. La prima edizione a stampa del Liber abbaci è stata curata da Baldassarre Boncompagni Ludovisi nel 1857, che si basò su un manoscritto di XIV secolo recante al suo interno una versione databile al 1228.

La riforma Gentile è una serie di atti normativi del Regno d'Italia che costituì una riforma scolastica organica varata in Italia. Prese il nome dall'ispiratore, il filosofo neoidealista Giovanni Gentile, Ministro della Pubblica Istruzione del governo Mussolini nel 1923 che la elaborò assieme a Giuseppe Lombardo Radice. Questa riforma prevedeva la formazione classica e umanistica, cui venne dato ampio spazio nel nuovo ordinamento, come unico mezzo di istruzione per formare le future classi dirigenti fasciste; così al Liceo classico venne attribuita molta importanza, e ricopriva un ruolo fondamentale quindi, nella formazione dirigenziale e amministrativa (Ogni dirigente, amministratore o dipendente pubblico doveva essere comunque tesserato al P.N.F.). «La più fascista» delle riforme, come la definì Mussolini, rimase sostanzialmente in vigore inalterata anche dopo l'avvento della Repubblica, fino a quando il parlamento italiano, con la legge 31 dicembre 1962 n. 1859, abolì la scuola di avviamento professionale creando la cosiddetta scuola media unificata.La riforma inoltre introdusse l'obbligo scolastico della qualifica di terza media.

L'Associazione Sportiva Livorno Calcio, meglio nota come Livorno, è una società calcistica italiana con sede nella città di Livorno. Nata nel 1915 come Unione Sportiva Livorno, venne rifondata nel 1991, quando assunse la denominazione attuale. Milita in Serie C, la terza divisione del campionato italiano. Ha disputato 29 stagioni al più alto livello del campionato italiano, 18 delle quali nella massima serie a girone unico. Dopo aver raggiunto la finalissima nazionale nella stagione 1919-1920, è stata una delle 18 squadre ammesse nel 1929 a disputare il primo campionato di A, dove vanta come miglior risultato il secondo posto conseguito nel 1942-1943. Nel suo palmarès annovera inoltre la vittoria di vari campionati e coppe minori nazionali, che gli hanno valso la 25ª miglior tradizione sportiva in Italia, mentre in campo europeo vanta una partecipazione alla Coppa UEFA nell'annata 2006-2007.

Principia Mathematica è un'opera sui fondamenti logici della matematica scritta da Alfred North Whitehead e Bertrand Russell. L'opera è divisa in tre volumi pubblicati nel 1910, 1912, e 1913 dalla Cambridge University Press. Nel 1927 è apparsa una seconda edizione con una nuova Introduzione e una nuova Appendice C. Una versione ridotta è apparsa nel 1962 col titolo Principia Mathematica to *56. L'Introduzione è stata tradotta in italiano da Paolo Parrini per i tipi de La Nuova Italia con il titolo Introduzione ai «Principia mathematica» (1977).

In geometria, il primo teorema di Euclide è un teorema attinente al triangolo rettangolo che deriva, assieme al secondo, dalla proposizione 8 del VI libro degli Elementi di Euclide; nei testi scolastici può essere enunciato in due modi diversi a seconda della proprietà che si desidera sottolineare: mediante l'equiestensione tra figure: mediante relazioni tra segmenti:

La storia della matematica ha origine con il concetto di numero e con le prime scoperte matematiche, proseguendo attraverso l'evoluzione nel corso dei secoli dei propri metodi e delle notazioni matematiche il cui uso si sussegue nel tempo. Un aspetto importante della matematica consiste nel fatto che essa si è sviluppata indipendentemente in culture completamente differenti arrivando in molti casi agli stessi risultati: spesso un contatto o una reciproca influenza tra popoli differenti ha portato all'introduzione di nuove idee e a un avanzamento delle conoscenze matematiche, a volte si è visto invece un regredire improvviso della cultura matematica presso alcuni popoli; la matematica moderna ha invece potuto avvalersi dei contributi di persone di tutti i paesi. L'attività svolta dai matematici moderni è molto diversa da quella dei primi matematici delle civiltà antiche; inizialmente la matematica si basò sul concetto di numero, concetto sviluppatosi nella preistoria. La matematica è stata infatti una tra le prime discipline a svilupparsi: evidenze archeologiche mostrano la conoscenza rudimentale di alcune nozioni matematiche molto prima dell'invenzione della scrittura.

La logica (dal greco λόγος, logos, ovvero "parola", "pensiero", "idea", "argomento", "ragione", da cui poi λογική, logiké) è lo studio del ragionamento e dell'argomentazione, rivolto in particolare a definire la correttezza dei procedimenti inferenziali del pensiero.

Il pensiero di Leibniz s'inserisce nel dibattito metafisico sulla sostanza, aperto da Cartesio e giunto alla sua conclusione con le filosofie di Spinoza e di Locke, alle quali Leibniz si opporrà.

Giovanni Gentile (Castelvetrano, 29 maggio 1875 – Firenze, 15 aprile 1944) è stato un filosofo, pedagogista, politico e accademico italiano. Fu insieme a Benedetto Croce uno dei maggiori esponenti del neoidealismo filosofico e dell'idealismo italiano, nonché un importante protagonista della cultura italiana nella prima metà del XX secolo, cofondatore dell'Istituto dell'Enciclopedia Italiana e, da ministro, artefice, nel 1923, della riforma della pubblica istruzione nota come Riforma Gentile. La sua filosofia è detta attualismo. Inoltre fu figura di spicco del fascismo italiano, considerato persino egli stesso l'inventore dell'ideologia del fascismo. In seguito alla sua adesione alla Repubblica Sociale Italiana, fu assassinato durante la seconda guerra mondiale da alcuni partigiani dei GAP.

In matematica, la prova del nove è un test di controllo, semplice ma non infallibile, per verificare l'esattezza del risultato di un'operazione aritmetica tra numeri interi, attraverso il raffronto delle radici numeriche degli operandi e del risultato. La prova è basata sulle proprietà congiunte della matematica modulare in modulo 9 (mod 9) e delle proprietà aritmetiche del numero 9 stesso, che permettono una notevole semplificazione del calcolo della congruità, in quanto coincidente con la radice numerica. La prova del nove solitamente si insegna nella scuola elementare quale scorciatoia per verificare la moltiplicazione tra due numeri, senza dover ripetere interamente l'algoritmo di computo generalmente lungo, ma può essere estesa anche alle altre operazioni addizione, sottrazione e divisione (con opportune precauzioni) comprese quella con resto. La prova del nove non assicura, però, completamente la certezza dell'esito: se è negativo, il risultato dell'operazione sarà senz'altro errato; se è positivo, vi è comunque l'11% di probabilità, 1 su 9, di un falso positivo, cioè che il risultato dell'operazione sia comunque errato nonostante l'esito positivo della prova.

+Europa (Più Europa, abbreviato +Eu o +E) è un partito politico italiano di orientamento europeista e liberale, nato dalla fusione fra i Radicali Italiani e dal movimento Forza Europa, che si è presentato con una propria lista elettorale alle elezioni politiche italiane del 2018.

I principi della dinamica sono le leggi fisiche su cui si fonda la dinamica newtoniana, che descrive le relazioni tra il moto di un corpo e gli enti che lo modificano. Sono validi in sistemi di riferimento inerziali e descrivono accuratamente il comportamento dei corpi che si muovono a velocità molto minori della velocità della luce, condizione in cui sono assimilabili con buona approssimazione ai principi più generali della relatività ristretta. Sono anche chiamati principi di Newton perché furono enunciati come assiomi da Isaac Newton nel suo trattato Philosophiae Naturalis Principia Mathematica, pur essendo il frutto di una lunga evoluzione da parte di numerosi scienziati che ne ha preceduto e seguito la pubblicazione; in particolare sono stati riformulati storicamente in vari modi, tra cui la formulazione lagrangiana e la formulazione hamiltoniana.

L'istituto tecnico è un percorso scolastico superiore italiano al quale lo studente può iscriversi dopo aver conseguito la licenza media.

Il Rinascimento a Urbino fu una delle declinazioni fondamentali del primo Rinascimento italiano. Durante la signoria di Federico da Montefeltro, dal 1444 al 1482, si sviluppò a corte un clima artistico fertile e vitale, grazie agli scambi culturali con numerosi centri della penisola e anche esteri, soprattutto fiamminghi. Il movimento culturale a Urbino si esauriva all'interno della corte, attorno al suo raffinatissimo principe, e pur elaborando soluzioni avanzatissime e d'avanguardia, non generò una vera e propria scuola locale, anche per il ricorso soprattutto ad artisti stranieri. Nonostante ciò il linguaggio urbinate, in virtù proprio della circolazione degli artisti, conobbe un'ampia diffusione, che ne fece una delle declinazioni chiave del Rinascimento italiano. Tra le caratteristiche base della sua cultura umanistica ci furono il tono inconfondibile fatto di misura e rigore, che ebbe protagonisti come Piero della Francesca, Luciano Laurana, Giusto di Gand, Pedro Berruguete, Francesco di Giorgio Martini, Fra Diamante. Secondo lo storico francese André Chastel, il Rinascimento urbinate, detto "matematico", fu una delle tre componenti fondamentali del Rinascimento delle origini, assieme a quello fiorentino, "filologico e filosofico", e quello padovano, "epigrafico ed archeologico". Dei tre era quello "più strettamente connesso alle arti". Nell'avvicinarsi al XVI secolo la città, pur restando un'isola di cultura raffinatissima, vide un impoverimento della sua vitalità nelle arti figurative. Nonostante ciò, a Urbino nacque e fece i primissimi passi uno dei grandi geni del Rinascimento maturo: Raffaello Sanzio. Da un punto di vista culturale e letterario invece Urbino restò a lungo uno degli ambienti più stimolanti d'Italia, come testimonia Baldassarre Castiglione, che alla corte di Guidobaldo ed Elisabetta da Montefeltro ambientò il suo Cortegiano.

In matematica il concetto di infinito (simbolo ∞ {\displaystyle \infty } ) ha molti significati, in correlazione con la nozione di limite, sia in analisi classica sia in analisi non standard. Nozioni di infinito sono usate in teoria degli insiemi e in geometria proiettiva.

Mathematica è un ambiente di calcolo simbolico e numerico multipiattaforma, ideato da Stephen Wolfram e successivamente sviluppato da un team di matematici e programmatori. Mathematica usa un potente linguaggio di programmazione interpretato, chiamato linguaggio Wolfram. Wolfram e il suo gruppo iniziarono a lavorare al programma nel 1986 e pubblicarono la prima versione nel 1988. La versione corrente è la 12.1, uscita il 18 marzo 2020. Il sistema Mathematica è disponibile per le piattaforme Windows, MacOS e Linux.

La matematica (dal greco μάθημα (máthema), traducibile con i termini "scienza", "conoscenza" o "apprendimento"; μαθηματικός (mathematikós) significa "incline ad apprendere") è la disciplina che studia le quantità (i numeri), lo spazio, le strutture e i calcoli.Per l'origine del termine occorre andare al vocabolo egizio maat, nella cui composizione appare il simbolo del cubito, strumento di misura lineare, un primo accostamento al concetto matematico. Simbolo geometrico di questo ordine è un rettangolo, da cui sorge la testa piumata della dea egizia Maat, personificazione dei concetti di ordine, verità e giustizia. Figlia di Ra, unico Uno, creatore di ogni cosa, la sua potenza demiurgica è limitata e ordinata da leggi naturali e matematiche. All'inizio del papiro di Rhind si trova questa affermazione: "Il calcolo accurato è la porta d'accesso alla conoscenza di tutte le cose e agli oscuri misteri". Il termine maat riappare in copto, in babilonese e in greco. In greco la radice ma, math, met entra nella composizione di vocaboli contenenti le idee di ragione, disciplina, scienza, istruzione, giusta misura, e in latino il termine materia indica ciò che può essere misurato. Col termine matematica di solito si designa la disciplina (e il relativo corpo di conoscenze) che studia problemi concernenti quantità, estensioni e figure spaziali, movimenti di corpi, e tutte le strutture che permettono di trattare questi aspetti in modo generale. La matematica fa largo uso degli strumenti della logica e sviluppa le proprie conoscenze nel quadro di sistemi ipotetico-deduttivi che, a partire da definizioni rigorose e da assiomi riguardanti proprietà degli oggetti definiti (risultati da un procedimento di astrazione, come triangoli, funzioni, vettori ecc.), raggiunge nuove certezze, per mezzo delle dimostrazioni, attorno a proprietà meno intuitive degli oggetti stessi (espresse dai teoremi). La potenza e la generalità dei risultati della matematica le ha reso l'appellativo di regina delle scienze: ogni disciplina scientifica o tecnica, dalla fisica all'ingegneria, dall'economia all'informatica, fa largo uso degli strumenti di analisi, di calcolo e di modellazione offerti dalla matematica.

Introduzione alla filosofia matematica è un'opera del filosofo gallese Bertrand Russell. Si propone di esporre i più basilari concetti che stanno alla base della matematica. Fu scritta durante il periodo di carcerazione scontato dall'autore per la sua partecipazione al movimento pacifista inglese durante la prima guerra mondiale. La trattazione è operata in una forma adatta ai non addetti ai lavori, evitando l'uso della simbologia più propria della materia e rinviando a Principia Mathematica per l'approfondimento degli aspetti tecnici più complessi. Il libro si sviluppa attraverso l'analisi di diversi argomenti, a ciascuno dei quali è dedicato un capitolo; tale percorso arriva in conclusione a mostrare l'arbitrarietà che secondo l'autore è presente in ogni tentativo di marcare un confine tra logica e matematica. L'indice dei capitoli: La serie dei numeri naturali La definizione di numero Il finito e l'induzione matematica La definizione di ordine Tipi di relazioni Similitudine tra relazioni I numeri razionali, reali e complessi Numeri cardinali infiniti Serie e ordinali infiniti Limiti e continuità Limiti e continuità delle funzioni Le selezioni e l'assioma moltiplicativo L'assioma dell'infinito e i tipi logici L'incompatibilità e l'assioma della deduzione Le funzioni proposizionali Le descrizioni Le classi Matematica e logica

Il lemma di Euclide è una generalizzazione della Proposizione 30 del Libro VII degli Elementi di Euclide. Il lemma afferma che Se un numero n, intero positivo, divide il prodotto di due numeri a e b, interi positivi, ed è coprimo con uno dei due (es. a), allora è divisore dell'altro (es. b).Utilizzando le usuali notazioni matematiche, ciò si può scrivere come segue: Se n|ab e MCD(n, a) = 1 allora n|b.La Proposizione 30, nota anche come primo teorema di Euclide, afferma: Se un numero primo divide il prodotto di due interi positivi, allora il numero primo divide almeno uno dei due interi positivi.Ciò si può scrivere come: Se p|ab allora p|a oppure p|b.Naturalmente, questo risultato si può dedurre immediatamente dal lemma di Euclide, in quanto un numero primo è coprimo con un numero intero se e solo se non lo divide. Spesso la Proposizione 30 viene chiamata lemma di Euclide in luogo della generalizzazione sopra citata. Un'applicazione molto comune del lemma di Euclide nei libri di testo di matematica è la dimostrazione del teorema fondamentale dell'aritmetica che, peraltro, può essere dimostrato senza farne uso.

Italia Europa Insieme, nota semplicemente come Insieme, è stata una lista elettorale italiana di ispirazione ulivista guidata da Giulio Santagata, presentata alle elezioni politiche italiane del 2018 all'interno della coalizione di centro-sinistra.

L'analisi matematica è il ramo della matematica che si occupa delle proprietà che emergono dalla scomposizione infinita di un oggetto denso. Si fonda sul calcolo infinitesimale, con il quale, attraverso le nozioni di limite e continuità, studia il comportamento locale di una funzione utilizzando gli strumenti del calcolo differenziale e del calcolo integrale. Introducendo per il calcolo concetti problematici, quali quello di infinito e di limite, si può passare all'indagine che le ha permesso di divenire basilare in diverse discipline scientifiche e tecniche (dalle scienze naturali all'ingegneria, dall'informatica all'economia), dove viene spesso coniugata con l'analisi numerica.

La matematica, nel corso della sua storia, è diventata una materia estremamente diversificata, di conseguenza si è reso necessario categorizzarne le aree. Nel frattempo sono sorti un certo numero di schemi di classificazione, e, anche se condividono alcune somiglianze, in essi sono presenti differenze dovute in parte ai diversi scopi per cui sono stati creati. Inoltre, dal momento che la matematica si evolve, questi schemi di classificazione devono a loro volta evolversi, anche a causa della scoperta di nuove aree o di collegamenti appena individuati tra quelle preesistenti. La classificazione inoltre è resa più difficile da parte di alcuni settori, spesso i più attivi, che si situano ai confini delle diverse aree. La matematica è divisa tradizionalmente in matematica pura, studiata per il suo interesse intrinseco, e matematica applicata, la matematica applicabile direttamente a problemi del mondo reale. Questa divisione non è sempre chiara e molti argomenti sono stati sviluppati nello studio della matematica pura per trovare in seguito inaspettate applicazioni. Più recentemente sono emerse divisioni di massima, come la matematica discreta e matematica computazionale.

La storia di Livorno, se confrontata con quelle delle altre città toscane, è sicuramente tra le più originali nel panorama regionale, in quanto slegata da uno sviluppo medievale che è comune alla maggior parte degli altri centri.Le origini dell'insediamento dal quale si è poi sviluppata la città sono comunque antiche e legate alla vicinanza con il principale scalo marittimo della Repubblica pisana. Tramontato il dominio di Pisa, i Medici decretarono l'ampliamento di Livorno, trasformando un piccolo villaggio nella più importante città italiana progettata e costruita tra la fine del XVI e l'inizio del XVII secolo.Principale porto del Granducato di Toscana e tra i più trafficati scali di tutto il bacino del Mediterraneo, Livorno divenne un rilevante centro economico animato da mercanti provenienti da qualsivoglia Nazione, come specificato dalle Leggi Livornine, che le conferirono i caratteri di città cosmopolita per eccellenza, anche durante il successivo dominio lorenese.Dopo l'unificazione e la crisi economica conseguente all'abolizione del porto franco, la città accolse numerose fabbriche di rilevanza nazionale, divenendo il maggiore centro industrializzato della Toscana.Fu duramente colpita dai bombardamenti aerei della seconda guerra mondiale, che, assieme alla ricostruzione, cancellarono parte delle sue principali vestigia, conferendole un aspetto moderno.

Giuseppe Francesco Antonio Alberti, noto come Giuseppe Antonio (Bologna, 29 gennaio 1712 – Perugia, 31 agosto 1768), è stato un perito di agrimensura, di architettura e di idrostatica bolognese.