biblio toscana

In matematica i numeri naturali sono quei numeri usati per contare e ordinare. Nel linguaggio comune i "numeri cardinali" sono quelli usati per contare e i "numeri ordinali" sono quelli usati per ordinare. I numeri naturali corrispondono all'insieme {0, 1, 2, 3, 4, …}. Essi vengono fatti corrispondere biunivocamente all'insieme dei numeri interi non negativi {0, +1, +2, +3, +4, …}. Talvolta vengono usati anche per indicare l'insieme dei numeri interi positivi {1, 2, 3, 4, …}.

La successione di Fibonacci (detta anche successione aurea), indicata con F n {\displaystyle F_{n}} o con F i b ( n ) {\displaystyle Fib(n)} , in matematica indica una successione di numeri interi in cui ciascun numero è la somma dei due precedenti, eccetto i primi due che sono, per definizione: F 0 = 0 {\displaystyle F_{0}=0} e F 1 = 1 {\displaystyle F_{1}=1} . Questa successione è definita ricorsivamente secondo la seguente regola: F 0 = 0 , {\displaystyle F_{0}=0,} F 1 = 1 , {\displaystyle F_{1}=1,} F n = F n − 1 + F n − 2 {\displaystyle F_{n}=F_{n-1}+F_{n-2}} (per ogni n>1)Gli elementi F n {\displaystyle F_{n}} sono anche detti numeri di Fibonacci. I primi termini della successione di Fibonacci, che prende il nome dal matematico pisano del XIII secolo Leonardo Fibonacci, sono: 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , … {\displaystyle 0,1,1,2,3,5,8,13,21,34,55,89,144,233,\dots }

In matematica, un numero primo (in breve anche primo) è un numero intero positivo che abbia esattamente due divisori distinti. In modo equivalente si può definire come un numero naturale maggiore di 1 che sia divisibile solamente per 1 e per sé stesso; al contrario, un numero maggiore di 1 che abbia più di due divisori è detto composto. Ad esempio 2, 3 e 5 sono primi mentre 4 e 6 non lo sono perché sono divisibili rispettivamente anche per 2 e per 2 e 3. L'unico numero primo pari è 2, in quanto tutti gli altri numeri pari sono divisibili per 2. La successione dei numeri primi comincia con 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…Quello di numero primo è uno dei concetti basilari della teoria dei numeri, la parte della matematica che studia i numeri interi: l'importanza sta nella possibilità di costruire con essi, attraverso la moltiplicazione, tutti gli altri numeri interi, nonché l'unicità di tale fattorizzazione. I primi sono inoltre infiniti e la loro distribuzione è tuttora oggetto di molte ricerche. I numeri primi sono oggetto di studio fin dall'antichità: i primi risultati risalgono agli antichi Greci, e in particolare agli Elementi di Euclide, scritti attorno al 300 a.C. Ciononostante, numerose congetture che li riguardano non sono state ancora dimostrate; tra le più note vi sono l'ipotesi di Riemann, la congettura di Goldbach e quella dei primi gemelli, indimostrate a più di un secolo dalla loro formulazione. Essi sono rilevanti anche in molti altri ambiti della matematica pura, come ad esempio l'algebra o la geometria; recentemente hanno assunto un'importanza cruciale anche nella matematica applicata, e in particolare nella crittografia.

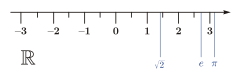
In matematica, i numeri reali possono essere descritti in maniera non formale come numeri ai quali è possibile attribuire uno sviluppo decimale finito o infinito, come π = 3 , 141592 … {\displaystyle \pi =3,141592\ldots } I numeri reali possono essere positivi, negativi o nulli e comprendono, come casi particolari, i numeri interi (come 12 {\displaystyle 12} ), i numeri razionali (come − 22 / 7 {\displaystyle -22/7} ) e i numeri irrazionali algebrici (come 2 {\displaystyle {\sqrt {2}}} ) e trascendenti (come π {\displaystyle \pi } ed e {\displaystyle e} ). Un numero reale razionale presenta uno sviluppo decimale finito o periodico; ad esempio 1 / 3 = 0 , 333333 … {\displaystyle 1/3=0,333333\ldots } è razionale. L'insieme dei numeri reali è generalmente indicato con la lettera R o R {\displaystyle \mathbb {R} } . I numeri reali possono essere messi in corrispondenza biunivoca con i punti di una retta, detta retta numerica o retta reale. La definizione formale dei numeri reali ha rappresentato uno degli sviluppi più significativi del XIX secolo. Tra le definizioni maggiormente adottate oggi figurano le classi di equivalenza di successioni di Cauchy di numeri razionali, le sezioni di Dedekind, una ridefinizione del termine "rappresentazione decimale" e una definizione assiomatica come unico campo archimedeo completo ordinato. I termini reale e immaginario sono stati introdotti ne La Géometrie di René Descartes (1637), relativamente allo studio delle radici delle equazioni. Per estensione diversi autori hanno cominciato a parlare di numeri reali e numeri immaginari. Nel 1874 appare un articolo fondamentale di Georg Cantor nel quale l'autore prende in considerazione l'insieme dei numeri reali dimostrando che tale insieme non è numerabile.

In matematica, un numero decimale periodico è un numero razionale che espresso in notazione decimale ha una stringa (finita) di cifre dopo la virgola che, da un certo punto in poi, si ripete all'infinito. Questa stringa ripetuta è detta periodo del numero. Molti numeri periodici hanno una stringa (finita) di cifre che non si ripete, prima che inizi il periodo, tale stringa non ripetuta è detta antiperiodo. Dato che la rappresentazione decimale del numero è infinita esistono, principalmente, due convenzioni per scrivere il numero in forma compatta. Si pone una linea continua sopra le cifre del periodo oppure si racchiudono le cifre che si ripetono tra parentesi tonde. Ad esempio 23,48771=23,4(8771)=23,487718771877187718771… Ogni numero decimale periodico, essendo una particolare rappresentazione di un numero razionale, può essere rappresentato mediante una frazione. Vale anche il viceversa, cioè che ogni numero razionale è periodico e quindi ogni frazione può essere espressa mediante un numero decimale periodico. Questo è immediato osservando che ogni numero con parte decimale finita in realtà è periodico di periodo 0. Ad esempio scrivendo 2,5=2,50=2,50000…

Cinematografo è un album-raccolta del 2010 che contiene 12 brani interpretati dal cantante Mario Merola.

Gli spettacoli nell'antica Roma erano numerosi, aperti a tutti i cittadini ed in genere gratuiti; alcuni di essi si distinguevano per la grandezza degli allestimenti e per la crudeltà. I Romani frequentavano di preferenza i combattimenti dei gladiatori, quelli con bestie feroci (venationes), le riproduzioni di battaglie navali (naumachia), le corse di carri, le gare di atletica, gli spettacoli teatrali dei mimi e le pantomime. Quarant'anni dopo l'invettiva di Giovenale (n. tra il 55 e il 60–m. dopo il 127) che rimpiangeva la sobrietà e la severità repubblicana di un popolo che ormai aspirava solo al panem et circenses, al pane e agli spettacoli, Frontone (100-166), quasi con le stesse parole, descriveva sconsolato la triste realtà: La classe dirigente romana considerava infatti suo compito primario quello di distribuire alimenti una volta al mese al popolo e di distrarlo e regolare il suo tempo libero con gli spettacoli gratuiti offerti nelle festività religiose o in ricorrenze laiche.