biblio toscana

L'algebra lineare è la branca della matematica che si occupa dello studio dei vettori, spazi vettoriali (o spazi lineari), trasformazioni lineari e sistemi di equazioni lineari. Gli spazi vettoriali sono un tema centrale nella matematica moderna; l'algebra lineare è usata ampiamente nell'algebra astratta, nella geometria e nell'analisi funzionale. L'algebra lineare ha inoltre una rappresentazione concreta nella geometria analitica. Con l'algebra lineare si studiano completamente tutti i fenomeni fisici "lineari", cioè quelli in cui intuitivamente non entrano in gioco distorsioni, turbolenze e fenomeni caotici in generale. Anche fenomeni più complessi, non solo della fisica ma anche delle scienze naturali e sociali, possono essere studiati e ricondotti con le dovute approssimazioni a un modello lineare.

L'algebra di Boole (anche detta algebra booleana o reticolo booleano), in matematica e logica matematica, è il ramo dell'algebra in cui le variabili possono assumere solamente i valori vero e falso (valori di verità), generalmente denotati rispettivamente come 1 e 0.

L'algebra (dall'arabo الجبر, al-ğabr, 'completamento') è una branca della matematica che tratta lo studio di strutture algebriche, relazioni e quantità.

La storia della matematica ha origine con il concetto di numero e con le prime scoperte matematiche, proseguendo attraverso l'evoluzione nel corso dei secoli dei propri metodi e delle notazioni matematiche il cui uso si sussegue nel tempo. Un aspetto importante della matematica consiste nel fatto che essa si è sviluppata indipendentemente in culture completamente differenti arrivando in molti casi agli stessi risultati: spesso un contatto o una reciproca influenza tra popoli differenti ha portato all'introduzione di nuove idee e a un avanzamento delle conoscenze matematiche, a volte si è visto invece un regredire improvviso della cultura matematica presso alcuni popoli; la matematica moderna ha invece potuto avvalersi dei contributi di persone di tutti i paesi. L'attività svolta dai matematici moderni è molto diversa da quella dei primi matematici delle civiltà antiche; inizialmente la matematica si basò sul concetto di numero, concetto sviluppatosi nella preistoria. La matematica è stata infatti una tra le prime discipline a svilupparsi: evidenze archeologiche mostrano la conoscenza rudimentale di alcune nozioni matematiche molto prima dell'invenzione della scrittura.

La matematica (dal greco μάθημα (máthema), traducibile con i termini "scienza", "conoscenza" o "apprendimento"; μαθηματικός (mathematikós) significa "incline ad apprendere") è la disciplina che studia le quantità (i numeri), lo spazio, le strutture e i calcoli.Per l'origine del termine occorre andare al vocabolo egizio maat, nella cui composizione appare il simbolo del cubito, strumento di misura lineare, un primo accostamento al concetto matematico. Simbolo geometrico di questo ordine è un rettangolo, da cui sorge la testa piumata della dea egizia Maat, personificazione dei concetti di ordine, verità e giustizia. Figlia di Ra, unico Uno, creatore di ogni cosa, la sua potenza demiurgica è limitata e ordinata da leggi naturali e matematiche. All'inizio del papiro di Rhind si trova questa affermazione: "Il calcolo accurato è la porta d'accesso alla conoscenza di tutte le cose e agli oscuri misteri". Il termine maat riappare in copto, in babilonese e in greco. In greco la radice ma, math, met entra nella composizione di vocaboli contenenti le idee di ragione, disciplina, scienza, istruzione, giusta misura, e in latino il termine materia indica ciò che può essere misurato. Col termine matematica di solito si designa la disciplina (e il relativo corpo di conoscenze) che studia problemi concernenti quantità, estensioni e figure spaziali, movimenti di corpi, e tutte le strutture che permettono di trattare questi aspetti in modo generale. La matematica fa largo uso degli strumenti della logica e sviluppa le proprie conoscenze nel quadro di sistemi ipotetico-deduttivi che, a partire da definizioni rigorose e da assiomi riguardanti proprietà degli oggetti definiti (risultati da un procedimento di astrazione, come triangoli, funzioni, vettori ecc.), raggiunge nuove certezze, per mezzo delle dimostrazioni, attorno a proprietà meno intuitive degli oggetti stessi (espresse dai teoremi). La potenza e la generalità dei risultati della matematica le ha reso l'appellativo di regina delle scienze: ogni disciplina scientifica o tecnica, dalla fisica all'ingegneria, dall'economia all'informatica, fa largo uso degli strumenti di analisi, di calcolo e di modellazione offerti dalla matematica.

Gli Stati Uniti d'America (comunemente indicati come Stati Uniti, in inglese: United States of America o anche solo United States; in sigla USA o anche U.S. e impropriamente con la sineddoche America) sono una repubblica federale dell'America settentrionale composta da cinquanta Stati e un distretto federale. I quarantotto stati contigui e il distretto di Washington D.C. (la capitale federale) occupano la fascia centrale dell'America settentrionale tra il Canada e il Messico e sono bagnati dall'oceano Atlantico a est e dall'oceano Pacifico a ovest. Con 9850476 km² in totale e circa 330 milioni di abitanti gli Stati Uniti sono il quarto paese al mondo per superficie e il terzo per popolazione. La geografia e il clima degli Stati Uniti sono estremamente vari, con deserti, pianure, foreste e montagne che sono anche sede di una grande varietà di fauna selvatica. È una delle nazioni più multietniche e multiculturali al mondo, prodotto di larga scala dell'immigrazione da molti Paesi. Storicamente i paleoamericani migrarono dall'Asia verso quelli che sono gli Stati Uniti circa 12 000 anni fa. La colonizzazione europea cominciò intorno al 1600 e venne per lo più dall'Inghilterra. Gli Stati Uniti d'America ebbero origine dalle tredici colonie britanniche situate lungo la costa atlantica. Le controversie tra la Gran Bretagna e le colonie sfociarono in un conflitto: il 4 luglio 1776 i delegati delle tredici colonie redassero ed approvarono all'unanimità la dichiarazione di indipendenza, che diede ufficialmente vita ad un nuovo Stato federale. La guerra di indipendenza americana, conclusasi con il riconoscimento dell'indipendenza degli Stati Uniti dal Regno di Gran Bretagna, è stata la prima guerra per l'indipendenza da una potenza coloniale europea. La Costituzione fu adottata il 17 settembre 1787 e da allora è stata emendata ventisette volte. I primi dieci emendamenti, collettivamente denominati «Dichiarazione dei diritti» (Bill of Rights), furono ratificati nel 1791 e garantiscono diritti civili e libertà fondamentali. Gli Stati Uniti intrapresero una vigorosa espansione per tutto il XIX secolo, spinti dalla controversa dottrina del destino manifesto. L'acquisizione di nuovi territori e l'ammissione di nuovi stati membri causarono anche numerose guerre con i popoli nativi. La guerra civile americana si concluse con l'abolizione della schiavitù negli Stati Uniti. Alla fine del XIX secolo gli Stati Uniti si estesero fino all'oceano Pacifico. La guerra ispano-americana e la prima guerra mondiale hanno confermato lo stato del paese come potenza militare globale. Gli Stati Uniti sono usciti dalla seconda guerra mondiale come una superpotenza globale, il primo paese dotato di armi nucleari e quale uno dei cinque membri permanenti del Consiglio di sicurezza delle Nazioni Unite. Dopo una grave crisi politica e sociale negli anni sessanta e settanta come conseguenza anche della sconfitta nella guerra del Vietnam, che sembrava minare il predominio mondiale statunitense, l'inattesa fine della guerra fredda e la dissoluzione dell'Unione Sovietica negli anni novanta hanno invece riconfermato il ruolo dominante degli Stati Uniti che sono rimasti l'unica superpotenza militare e politica mondiale. Gli Stati Uniti sono un Paese sviluppato, con una stima nel 2017 del prodotto interno lordo (PIL) di 19,39 migliaia di miliardi di dollari (il 23% del PIL mondiale a parità di potere di acquisto, a partire dal 2011). Il PIL pro capite degli Stati Uniti è stato il sesto più alto del mondo dal 2010, anche se la disparità di reddito del continente americano è stata anche classificata la più alta all'interno dell'OCSE e i paesi dalla Banca Mondiale. L'economia è alimentata da un'abbondanza di risorse naturali, numerose infrastrutture ed elevata produttività. Il paese rappresenta il 39% della spesa militare mondiale, essendo la prima potenza economica e militare, una forza politica guida nel mondo e al primo posto nel settore della ricerca scientifica e dell'innovazione tecnologica, ma anche uno stato sociale ridotto rispetto a molti altri paesi del mondo occidentale.

Il calcolo infinitesimale è la branca fondante dell'analisi matematica che studia il "comportamento locale" di una funzione tramite le nozioni di continuità e limite, usato in quasi tutti i campi della matematica e della fisica, e della scienza in generale. Le funzioni a cui si applica sono a variabile reale o complessa. Tramite la nozione di limite, il calcolo infinitesimale definisce e studia le nozioni di convergenza di una successione o di una serie, continuità, derivata e integrale.

In matematica, il concetto di limite serve a descrivere l'andamento di una funzione all'avvicinarsi del suo argomento a un dato valore (limite di una funzione) oppure l'andamento di una successione al crescere illimitato dell'indice (limite di una successione). I limiti si utilizzano in tutti i rami dell'analisi matematica; sono usati ad esempio per definire la continuità, la derivazione e l'integrazione. Il concetto di limite di una funzione, più generale del limite di una successione, può essere generalizzato da quello di limite di un filtro.

La matematica, nel corso della sua storia, è diventata una materia estremamente diversificata, di conseguenza si è reso necessario categorizzarne le aree. Nel frattempo sono sorti un certo numero di schemi di classificazione, e, anche se condividono alcune somiglianze, in essi sono presenti differenze dovute in parte ai diversi scopi per cui sono stati creati. Inoltre, dal momento che la matematica si evolve, questi schemi di classificazione devono a loro volta evolversi, anche a causa della scoperta di nuove aree o di collegamenti appena individuati tra quelle preesistenti. La classificazione inoltre è resa più difficile da parte di alcuni settori, spesso i più attivi, che si situano ai confini delle diverse aree. La matematica è divisa tradizionalmente in matematica pura, studiata per il suo interesse intrinseco, e matematica applicata, la matematica applicabile direttamente a problemi del mondo reale. Questa divisione non è sempre chiara e molti argomenti sono stati sviluppati nello studio della matematica pura per trovare in seguito inaspettate applicazioni. Più recentemente sono emerse divisioni di massima, come la matematica discreta e matematica computazionale.

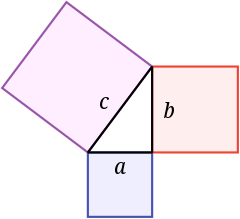
Il teorema di Pitagora è un teorema della geometria euclidea che stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo. Si può considerare un caso speciale, per i triangoli rettangoli, del teorema del coseno.

Bartolomeo Veratti (Modena, 1809 – Modena, 2 aprile 1889) è stato un giurista, giornalista e filologo italiano, ma viene ricordato soprattutto per il suo importante contributo alla storia delle matematiche.

La storia del computer è l'evoluzione dell'apparecchio elettronico destinato all'elaborazione dei dati, privo di capacità decisionale o discrezionale, che compie determinate operazioni secondo procedure prestabilite o programmi.

In matematica si definisce equazione di quarto grado o quartica quell'equazione algebrica in cui il grado più alto dell'incognita è il quarto. Nella forma canonica, assume la forma: a x 4 + b x 3 + c x 2 + d x + e = 0 (con a ≠ 0 ) . {\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0\qquad {\mbox{(con }}a\neq 0).} La prima soluzione generale dell'equazione di quarto grado si deve al matematico italiano Ferrari, pubblicata però nel 1545 nell'Artis Magnae sive de regulis algebraicis di Cardano, che conteneva anche il metodo risolutivo dell'equazione di terzo grado. Si profuse allora grande impegno nel trovare le soluzioni generali di equazioni di quinto grado e superiore, ma invano: solo due secoli e mezzo dopo, i lavori di Ruffini del 1799, in maniera incompleta, e di Abel nel 1824, in maniera esaustiva, costituiscono complessivamente quello oggi noto come Teorema di Abel-Ruffini. In particolare Lagrange trovò che l'equazione risolvente di un'equazione di quinto grado è un'equazione di sesto, ricollegandosi ai risultati di Galois nella teoria dei gruppi.

L'aritmetica (dal greco ἀριθμός = numero) è la più antica branca della matematica, quella che studia le proprietà elementari delle operazioni aritmetiche sui numeri, specialmente i numeri interi. È praticata quotidianamente da tutti per scopi molto semplici, come contare oggetti, valutare costi, stabilire distanze; viene utilizzata anche per scopi avanzati, ad esempio in complessi calcoli finanziari o nella tecnologia delle comunicazioni (crittografia). I matematici talvolta usano il termine aritmetica per indicare la teoria dei numeri; questa disciplina però tratta problemi più avanzati e specifici rispetto all'aritmetica elementare e non viene presa in considerazione nel presente articolo.

In algebra lineare, il determinante è una funzione che associa ad ogni matrice quadrata A {\displaystyle A} uno scalare che ne sintetizza alcune proprietà algebriche. Storicamente i determinanti sono stati studiati prima delle matrici. In origine il determinante è stata considerata una costruzione riguardante un sistema di equazioni lineari. Questa funzione del sistema "determina" se il sistema possiede una soluzione unica (fatto che si verifica se e solo se il determinante è diverso da zero). Per questo scopo Girolamo Cardano ha considerato determinanti di ordine 2 verso la fine del secolo XVI e Leibniz ne ha considerati di ordini superiori circa 100 anni più tardi. Sulle sue orme Gabriel Cramer (1750) ha esteso la loro teoria, sempre in relazione ai sistemi di equazioni. La legge di ricorrenza per il loro calcolo è stata annunciata per la prima volta da Étienne Bézout (1764). Vandermonde (1771) per primo ha trattato i determinanti come funzioni autonome. Laplace (1772) ha formulato il procedimento generale per lo sviluppo di un determinante in termini dei suoi minori complementari: Vandermonde ne aveva dato un caso particolare in precedenza. Immediatamente dopo Joseph-Louis Lagrange (1773) ha trattato i determinanti del secondo e del terzo ordine. Lagrange è stato il primo ad applicare i determinanti a questioni al di fuori della teoria della eliminazione delle variabili; egli ha dimostrato molti casi di identità di portata generale. Carl Friedrich Gauss (1801) ha dato il successivo contributo. Come Lagrange egli ha utilizzato ampiamente i determinanti nella teoria dei numeri. Fu lui ad introdurre il termine determinante (Laplace aveva utilizzato risultante), non con il significato attuale generale, ma applicandolo al discriminante di una quantica. Gauss è arrivato anche alla nozione di determinanti reciproci (inversi), ed è giunto molto vicino al teorema di moltiplicazione. Il successivo contributore di rilievo è Jacques Philippe Marie Binet (1811, 1812), il quale ha enunciato formalmente il teorema che concerne il prodotto di due matrici di m {\displaystyle m} colonne ed n {\displaystyle n} righe, che nel caso particolare m = n {\displaystyle m=n} si riduce al teorema di moltiplicazione. Lo stesso giorno 30 novembre 1812 nel quale Binet presentava il suo articolo alla Academie de Sciences, Augustin-Louis Cauchy ne presentava uno suo sullo stesso argomento (vedi formula di Cauchy-Binet). Nel suo lavoro Cauchy utilizza il termine determinant nel suo significato attuale, riassume e semplifica quello che era finora noto sull'argomento, migliora le notazioni e presenta il teorema di moltiplicazione con una dimostrazione più soddisfacente di quella di Binet. Con lui inizia la teoria nella sua generalità. La successiva figura di spicco è Carl Gustav Jakob Jacobi che studia l'argomento dal 1827. Egli per primo tratta il determinante funzionale che successivamente Sylvester chiamerà Jacobiano e nella sua memoria sul Journal di Crelle fino al 1841 egli si occupa specialmente questo argomento insieme alla classe di funzioni alternanti che Sylvester chiama, appunto, alternanti. Nel periodo delle ultime memorie di Jacobi, Sylvester (1839) e Arthur Cayley cominciano a lavorare su questi temi. Lo studio dei determinanti di matrici di forma speciale è stato il naturale sbocco del completamento della teoria generale. Determinanti asimmetrici sono stati studiati da Lebesgue, Hesse e Sylvester; determinanti persimmetrici da Sylvester e Hermann Hankel; circolanti da Eugène Charles Catalan, William Spottiswoode, James Whitbread Lee Glaisher e Scott; determinanti antisimmetrici e pfaffiani, in connessione con la teoria delle trasformazione ortogonale, da Cayley; continuanti da Sylvester; wronskiani (battezzati in questo modo da Thomas Muir) da Elwin Bruno Christoffel e Ferdinand Georg Frobenius; determinanti composti da Sylvester, Reiss e Picquet; jacobiani ed hessiani da Sylvester; determinanti simmetrici a sinistra da Trudi. Il primo libro di testo su questi argomenti è stato scritto da Spottiswoode. Negli Stati Uniti sono comparsi i primi trattati di Hanus (1886) e Weld (1893).

L'algebra elementare è la branca della matematica che studia il calcolo letterale, cioè studia i monomi e i polinomi ed estende ad essi le operazioni aritmetiche, dette in questo contesto operazioni algebriche. Ciò è di grande utilità perché: consente la formulazione generale di leggi aritmetiche (come a + b = b + a per ogni a e b), e quindi è il primo passo per un'esplorazione sistematica delle proprietà del sistema dei numeri reali; consente di riferirsi a numeri incogniti e quindi di formulare delle equazioni e di sviluppare tecniche per risolverle (per esempio: "trova un numero x {\displaystyle x} tale che 3 ⋅ x + 2 = 10 {\displaystyle 3\cdot x+2=10} ); consente la formulazione di relazioni funzionali (come la seguente: "se si vendono x {\displaystyle x} biglietti, allora il profitto sarà 10 x − 5 {\displaystyle 10x-5} euro").Un'espressione algebrica può contenere numeri, variabili ed operazioni aritmetiche; esempi sono a + 3 {\displaystyle a+3} e x 2 − 3 {\displaystyle x^{2}-3} . Un'equazione è l'affermazione che due espressioni sono uguali in alcuni casi. Alcune equazioni sono vere per ogni valore delle variabili incognite (per esempio a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} ); esse sono conosciute come identità. Altre equazioni contengono dei simboli per le variabili incognite e siamo quindi interessati a trovare quei particolari valori che rendono vera l'uguaglianza: x 2 − 1 = 4 {\displaystyle x^{2}-1=4} . Essi sono detti soluzioni o zeri dell'equazione.

Un'espressione matematica è un insieme di numeri legati da segni di operazioni matematiche, detti operatori matematici.

Angiolo Procissi (Prato, 6 dicembre 1908 – Firenze, 28 agosto 1987) è stato un matematico e storico della matematica italiano.

In matematica, un campo è una struttura algebrica composta da un insieme non vuoto K {\displaystyle K} e da due operazioni binarie interne, chiamate somma e prodotto e indicate di solito rispettivamente con + {\displaystyle +} e ∗ {\displaystyle *} . Queste godono di proprietà assimilabili a quelle verificate da somma e prodotto sui numeri razionali o reali o anche complessi. Il campo è una struttura algebrica basilare in matematica, necessaria per lo studio approfondito dei polinomi e delle loro radici, e per la definizione degli spazi vettoriali. Nel contesto degli spazi vettoriali un elemento di un campo è detto scalare.

Il teorema di Perron-Frobenius afferma che, se A {\displaystyle A} è una matrice non negativa (cioè, con tutti gli elementi maggiori o uguali a zero) primitiva e irriducibile allora L'autovalore di modulo massimo λ {\displaystyle \lambda } di A {\displaystyle A} è reale positivo Esso è un autovalore semplice L'autovettore corrispondente ha tutte le componenti positive L'autovettore corrispondente è l'unico autovettore non negativo di A {\displaystyle A} L'autovalore di modulo massimo, visto come funzione ρ ( A ) {\displaystyle \rho (A)} della matrice A {\displaystyle A} , è una funzione strettamente crescente in ognuno dei suoi elementi: cioè, se B ≥ A {\displaystyle B\geq A} (s'intende che tale disuguaglianza valga elemento per elemento) e B ≠ A {\displaystyle B\neq A} , allora ρ ( B ) > ρ ( A ) {\displaystyle \rho (B)>\rho (A)} Il teorema di Perron-Frobenius è un risultato abbastanza potente ma elementare di algebra lineare che solitamente non si vede nei primi corsi. Una sua applicazione è per esempio quella di assicurare l'esistenza di misure invarianti per catene di Markov finite.

L'algebra di Grassmann o algebra esterna di un dato spazio vettoriale V {\displaystyle V} sopra un campo K {\displaystyle K} è una certa algebra associativa dotata di elemento neutro, generata dalla definizione di un prodotto esterno o prodotto wedge scritto come ∧ {\displaystyle \wedge } . È denotata con ( Λ ( V ) , ∧ ) {\displaystyle \left(\Lambda (V),\,\wedge \right)} e contiene V {\displaystyle V} come sottospazio. Le algebre esterne sono molto utilizzate nella geometria differenziale e nella geometria algebrica (algebra esterna delle forme differenziali) oltre che nell'algebra multilineare e nei settori collegati. Il prodotto esterno è associativo e bilineare; la sua proprietà essenziale è che sia alternante su V {\displaystyle V} : v ∧ v = 0 {\displaystyle v\wedge v=0} per tutti i vettori v ∈ V {\displaystyle v\in V} ossia: u ∧ v = − v ∧ u {\displaystyle u\wedge v=-v\wedge u} per ogni vettore u , v ∈ V {\displaystyle u,v\in V} , e v 1 ∧ v 2 ∧ ⋯ ∧ v k = 0 {\displaystyle v_{1}\wedge v_{2}\wedge \cdots \wedge v_{k}=0} qualora v 1 , … , v k ∈ V {\displaystyle v_{1},\ldots ,v_{k}\in V} siano linearmente dipendenti.Il concetto di prodotto esterno generalizza i concetti di prodotto vettoriale e di triplo prodotto scalare della geometria euclidea tridimensionale. Esso fornisce un modo algebrico astratto, indipendente dalla scelta di una base, per descrivere il determinante e i minori di una trasformazione lineare. È quindi collegato alle idee di indipendenza lineare e di rango. L'algebra di Grassmann è l'esempio prototipo di algebre supercommutative. Queste sono algebre con una decomposizione in variabili pari e dispari che soddisfa una versione graduata della commutatività (in particolare, elementi dispari anticommutano).

Pierre de Fermat (Beaumont-de-Lomagne, 17 agosto 1601 – Castres, 12 gennaio 1665) è stato un matematico e magistrato francese. Fu tra i principali matematici della prima metà del XVII secolo e dette importanti contributi allo sviluppo della matematica moderna: con il suo metodo per la individuazione dei massimi e dei minimi delle funzioni precorse gli sviluppi del calcolo differenziale; fece ricerche di grande importanza sulla futura teoria dei numeri, iniziate durante la preparazione di un'edizione della Arithmetica di Diofanto di Alessandria, su cui scrisse note ed osservazioni contenenti numerosi teoremi. Proprio in una di queste osservazioni "a margine" enunciò il cosiddetto ultimo teorema di Fermat (che credeva, molto probabilmente a torto, di aver dimostrato), che è rimasto indimostrato per più di 300 anni, fino al lavoro di Andrew Wiles nel 1994; scoprì, indipendentemente da Cartesio, i principi fondamentali della geometria analitica e, attraverso la corrispondenza con Blaise Pascal, fu uno dei fondatori della teoria della probabilità.

In matematica, la teoria di Galois è una branca superiore dell'algebra astratta. Al livello più semplice usa i gruppi di permutazioni per descrivere come le varie radici di un dato polinomio sono collegate le une con le altre. Questo era l'originale punto di vista di Évariste Galois. L'approccio moderno alla teoria di Galois, sviluppato da Richard Dedekind, Leopold Kronecker e Emil Artin fra gli altri, comprende lo studio degli automorfismi delle estensioni di campi. Ulteriori astrazioni della teoria di Galois si ottengono con la teoria delle connessioni di Galois.

Domenico Amanzio (Marano di Napoli, 2 febbraio 1854 – Napoli, 17 agosto 1908) è stato un matematico e astronomo italiano.

In matematica, in particolare in algebra, un campo finito (detto a volte anche campo di Galois) è un campo che contiene un numero finito di elementi. I campi finiti sono importanti in teoria dei numeri, geometria algebrica, teoria di Galois, in crittografia e in teoria dei codici. I campi finiti sono completamente classificati.

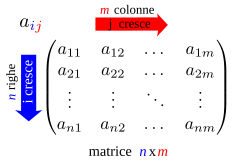
In matematica, in particolare in algebra lineare, una matrice è una tabella ordinata di elementi. Ad esempio: ( 1 0 5 1 − 2 0 ) {\displaystyle {\begin{pmatrix}1&0&5\\1&-2&0\end{pmatrix}}} Le matrici sono ampiamente usate in matematica e in tutte le scienze per la loro capacità di rappresentare in maniera utile e concisa diversi oggetti matematici, come valori che dipendono da due parametri o anche sistemi lineari, cosa, quest'ultima, che le rende uno strumento centrale dell'analisi matematica.

Il concetto di numero risale presumibilmente agli albori della civiltà. Rappresentare una quantità con un simbolo ha permesso al pensiero umano di raggiungere mete notevoli. La possibilità di indagare in ambiti non accessibili direttamente all'esperienza o ai sensi, come ad esempio la decimilionesima cifra decimale di pi greco, è dovuta alla nascita dell'astrazione matematica. Uno dei reperti più interessanti dell'archeologia, dal punto di vista della matematica, è stato rinvenuto a Ishango, sul lago Edoardo al confine tra Zaire e Uganda. Si tratta di un manico in osso, detto Osso d'Ishango, ora al Museo di Storia Naturale di Bruxelles, risalente a circa ventimila anni fa (periodo paleolitico); esso presenta incisioni raccolte in diversi gruppi, su tre righe, così disposte: riga a): 9 19 21 11 - totale 60 riga b): 19 17 13 11 - totale 60 riga c): 7 5 5 10 8 4 6 3 - totale 48Sebbene non vi sia accordo sulla natura delle incisioni, si può quasi sicuramente affermare che la popolazione paleolitica di Ishango possedeva il concetto di numero.

In matematica ed in particolare nell'algebra e nelle sue applicazioni i logaritmi discreti sono il corrispettivo dei logaritmi ordinari per l'aritmetica modulare. Il problema del calcolo dei logaritmi discreti ha notevoli somiglianze con quello della fattorizzazione dei numeri interi, in quanto entrambi i problemi sono supposti difficili (non sono noti algoritmi che li risolvono in tempo polinomiale), algoritmi dell'uno sono spesso adattati all'altro e viceversa, ed entrambi sono stati utilizzati come base teorica per la costruzione di sistemi crittografici. In particolare, il logaritmo discreto trova applicazione nella crittografia basata su curve ellittiche. Tali sistemi crittografici fondano la propria sicurezza sulla supposta difficoltà di tali problemi.

La teoria degli insiemi è una teoria matematica posta ai fondamenti della matematica stessa, collocandosi nell'ambito della logica matematica. Prima della prima metà del XIX secolo la nozione di insieme veniva considerata solo come qualcosa di intuitivo e generico. La nozione è stata sviluppata nella seconda metà del XIX secolo dal matematico tedesco Georg Cantor, è stata al centro dei dibattiti sui fondamenti dal 1890 al 1930 ed ha ricevuto le prime sistemazioni assiomatiche per merito di Ernst Zermelo, Adolf Fraenkel, Paul Bernays, Kurt Gödel, John von Neumann e Thoralf Skolem, Gottlob Frege (le convenzioni linguistico-formali, come il quantificatore universale ed esistenziale) e Giuseppe Peano (notazione e sintassi). In questo periodo si sono assestati due sistemi di assiomi chiamati sistema assiomatico di Zermelo-Fraenkel e sistema assiomatico di Von Neumann-Bernays-Gödel. Successivamente si sono affrontate le tematiche riguardanti il problema della completezza dei sistemi di assiomi (v. teorema di incompletezza di Gödel), i rapporti con la teoria della calcolabilità (vedasi anche macchina di Turing) e la compatibilità dei sistemi di assiomi con l'assioma della scelta e con assiomi equivalenti o simili. Accanto a differenti consolidate teorie formali degli insiemi (vedi anche teoria assiomatica degli insiemi) esistono esposizioni più intuitive che costituiscono la cosiddetta teoria ingenua degli insiemi. Elenchiamo le entità principali della teoria degli insiemi.

Un numero complesso è definito come un numero della forma x + y i {\displaystyle x+yi} con x {\displaystyle x} e y {\displaystyle y} numeri reali e i {\displaystyle i} una soluzione dell'equazione x 2 = − 1 {\displaystyle x^{2}=-1} ed è detta unità immaginaria. I numeri complessi sono usati in tutti i campi della matematica, in molti campi della fisica (notoriamente in meccanica quantistica), nonché in ingegneria, specialmente in elettronica/telecomunicazioni o elettrotecnica, per la loro utilità nel rappresentare onde elettromagnetiche e correnti elettriche ad andamento temporale sinusoidale. In matematica i numeri complessi formano un campo (nonché un'algebra reale bidimensionale) e sono generalmente visualizzati come punti di un piano, detto piano complesso. La proprietà più importante dei numeri complessi è basata sul teorema fondamentale dell'algebra, secondo il quale qualunque equazione polinomiale di grado n {\displaystyle n} ha n {\displaystyle n} soluzioni complesse, non necessariamente distinte.

Il Liber quadratorum di Leonardo Fibonacci è un importante trattato di argomento algebrico in lingua latina. L'opera, che fu pubblicata intorno al 1225, si apre con un'epistola di dedica a Federico II di Hohenstaufen, in cui si afferma che fu il maestro Domenico, già destinatario della Practica geometriae, a presentare il matematico all'imperatore: Nel Liber quadratorum Fibonacci discute la risoluzione di due quesiti: il primo, che gli fu posto dal maestro Giovanni da Palermo, consiste nel calcolare un numero quadrato tale che, aumentato o diminuito di cinque, dia come risultato un numero quadrato; il secondo, che invece gli fu posto dal maestro Teodoro di Antiochia, consiste nel rinvenire tre numeri «tali che la loro somma, aggiunta al quadrato del primo, sia un numero quadrato; che questo numero quadrato, aumentato del quadrato del secondo, sia un numero quadrato e che anche quest’ultimo, sommato al quadrato del terzo, dia un quadrato (equazioni pitagoriche)»

In algebra lineare, il determinante di una matrice quadrata A {\displaystyle A} è un numero che descrive alcune proprietà algebriche e geometriche della matrice. Esso viene generalmente indicato con det ( A ) {\displaystyle \det(A)} e, a volte, con | A | {\displaystyle |A|} . Quest'ultima notazione è più compatta, ma anche più ambigua, in quanto utilizzata talvolta per descrivere una norma della matrice.Il determinante è un potente strumento usato in vari settori della matematica: innanzitutto nello studio dei sistemi di equazioni lineari, quindi nel calcolo infinitesimale a più dimensioni (ad esempio nello Jacobiano), nel calcolo tensoriale, nella geometria differenziale, nella teoria combinatoria, ecc. Il significato geometrico principale del determinante si ottiene interpretando la matrice quadrata A {\displaystyle A} di ordine n {\displaystyle n} come trasformazione lineare di uno spazio vettoriale a n {\displaystyle n} dimensioni: con questa interpretazione, il valore assoluto di det ( A ) {\displaystyle \det(A)} è il fattore con cui vengono modificati i volumi degli oggetti contenuti nello spazio (anche se ciò è improprio senza considerare il significato di misura). Se è diverso da zero, il segno del determinante indica inoltre se la trasformazione A {\displaystyle A} preserva o cambia l'orientazione dello spazio rispetto agli assi di riferimento.

In matematica, un numero primo (in breve anche primo) è un numero intero positivo che abbia esattamente due divisori distinti. In modo equivalente si può definire come un numero naturale maggiore di 1 che sia divisibile solamente per 1 e per sé stesso; al contrario, un numero maggiore di 1 che abbia più di due divisori è detto composto. Ad esempio 2, 3 e 5 sono primi mentre 4 e 6 non lo sono perché sono divisibili rispettivamente anche per 2 e per 2 e 3. L'unico numero primo pari è 2, in quanto tutti gli altri numeri pari sono divisibili per 2. La successione dei numeri primi comincia con 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…Quello di numero primo è uno dei concetti basilari della teoria dei numeri, la parte della matematica che studia i numeri interi: l'importanza sta nella possibilità di costruire con essi, attraverso la moltiplicazione, tutti gli altri numeri interi, nonché l'unicità di tale fattorizzazione. I primi sono inoltre infiniti e la loro distribuzione è tuttora oggetto di molte ricerche. I numeri primi sono oggetto di studio fin dall'antichità: i primi risultati risalgono agli antichi Greci, e in particolare agli Elementi di Euclide, scritti attorno al 300 a.C. Ciononostante, numerose congetture che li riguardano non sono state ancora dimostrate; tra le più note vi sono l'ipotesi di Riemann, la congettura di Goldbach e quella dei primi gemelli, indimostrate a più di un secolo dalla loro formulazione. Essi sono rilevanti anche in molti altri ambiti della matematica pura, come ad esempio l'algebra o la geometria; recentemente hanno assunto un'importanza cruciale anche nella matematica applicata, e in particolare nella crittografia.

Euclide (in greco antico: Εὐκλείδης, Eukléidēs; IV secolo a.C. – III secolo a.C.) è stato un matematico e filosofo greco antico. Si occupò di vari ambiti, dall’ottica all’astronomia, dalla musica alla meccanica, oltre, ovviamente, alla matematica. Gli "Elementi", il suo lavoro più noto, è una delle più influenti opere di tutta la storia della matematica e fu uno dei principali testi per l'insegnamento della geometria dalla sua pubblicazione fino agli inizi del ‘900.

L'Italia (/iˈtalja/, ), ufficialmente Repubblica Italiana, è uno Stato situato nell'Europa meridionale, il cui territorio coincide in gran parte con l'omonima regione geografica. L'Italia è una repubblica parlamentare e conta una popolazione di circa 60 milioni di abitanti. La capitale è Roma. La parte continentale, delimitata dall'arco alpino, confina a nord, da ovest a est, con Francia, Svizzera, Austria e Slovenia; il resto del territorio, circondato dai mari Ligure, Tirreno, Ionio e Adriatico, si protende nel mar Mediterraneo, occupando la penisola italiana e numerose isole (le maggiori sono Sicilia e Sardegna), per un totale di 302072,84 km². Gli Stati della Città del Vaticano e di San Marino sono enclavi della Repubblica mentre Campione d'Italia è l'unica exclave italiana. Con l'ascesa di Roma, che fu capitale della Repubblica romana e poi dell'Impero romano, si ebbe il primo processo di unificazione della penisola, destinata a rimanere per secoli il centro politico e culturale della civiltà occidentale. Dopo la caduta dell'Impero romano d'Occidente, l'Italia medievale fu soggetta a invasioni e dominazioni di popolazioni germaniche, come gli Ostrogoti, i Longobardi e i Normanni, perdendo la propria unità politica. Nel XV secolo, con la diffusione del Rinascimento, ridivenne il centro culturale del mondo occidentale, ma dopo le guerre d'Italia del XVI secolo ricadde sotto l'egemonia delle potenze straniere, quali Francia, Spagna e Austria. Durante il Risorgimento gli italiani combatterono per l'indipendenza nazionale e per l'Unità d'Italia, finché nel 1861 fu proclamato il Regno d'Italia, che completò la riunificazione con la presa di Roma del 20 settembre 1870 e la vittoria nella prima guerra mondiale. Dal 1882 al 1960 l'Italia ha posseduto un impero coloniale. Nel 1946, dopo il ventennio fascista, la sconfitta nella seconda guerra mondiale e la guerra civile, a seguito di un referendum istituzionale lo Stato italiano divenne una repubblica. Nel 2020 l'Italia, ottava potenza economica mondiale e terza nell'Unione europea, è un paese con un alto standard di vita: l'indice di sviluppo umano è molto alto, 0.883, e la speranza di vita è di 83,4 anni. È membro fondatore dell'Unione europea, della NATO, del Consiglio d'Europa e dell'OCSE; aderisce all'ONU e al trattato di Schengen. È inoltre membro del G7 e del G20, partecipa al progetto di condivisione nucleare della NATO, è una grande potenza regionale europea, in grado di esercitare influenza politica anche su scelte e decisioni di ordine extra-europeo e globale, e si colloca in nona posizione nel mondo per spesa militare. In virtù della sua storia ultramillenaria, l'Italia vanta insieme alla Cina il maggior numero di siti dichiarati patrimonio dell'umanità dall'UNESCO.

L'ultimo teorema di Fermat, più correttamente definibile come ultima congettura di Fermat, non essendo dimostrata all'epoca, afferma che non esistono soluzioni intere positive all'equazione: a n + b n = c n {\displaystyle a^{n}+b^{n}=c^{n}} se n > 2 {\displaystyle n>2} .

In matematica, per risolvere un'equazione si intende la ricerca degli elementi (numeri, funzioni, insieme, ecc.) che soddisfino la rispettiva equazione (due espressioni unite da un'uguaglianza). Queste espressioni contengono una o più incognite, che sono variabili libere per le quali sono cercati i valori che fanno sì che la condizione espressa dall'equazione sia soddisfatta. Per essere precisi, di solito si intende che questi valori non sono necessariamente valori reali, ma, in realtà, spesso sono espressioni matematiche. Una soluzione dell'equazione è un'assegnazione di espressioni alle incognite che soddisfi l'equazione, in altre parole, quando questi risultati vengono sostituiti alle incognite, l'equazione diventa una tautologia (un'affermazione dimostrabilmente vera). Per esempio, l'equazione x + y = 2 x − 1 {\displaystyle x+y=2x-1} è risolvibile nell'incognita x {\displaystyle x} da x = y + 1 , {\displaystyle x=y+1,} in quanto sostituendo x {\displaystyle x} con y + 1 {\displaystyle y+1} l'equazione sarà ( y + 1 ) + y = 2 ( y + 1 ) − 1 {\displaystyle (y+1)+y=2(y+1)-1} , un'affermazione vera. È anche possibile prendere in considerazione la variabile y {\displaystyle y} , e quindi la soluzione questa volta sarà y = x − 1 {\displaystyle y=x-1} . Oppure x {\displaystyle x} and y {\displaystyle y} possono essere trattate entrambe come incognite, e in questo caso ci sono più soluzioni dell'equazione, tra cui, ad esempio, ( x ; y ) = ( 1 ; 0 ) {\displaystyle (x;y)=(1;0)} (cioè x = 1 {\displaystyle x=1} e y = 0 {\displaystyle y=0} ), ( x ; y ) = ( 2 ; 1 ) {\displaystyle (x;y)=(2;1)} , ed in generale ( x ; y ) = ( a + 1 ; a ) {\displaystyle (x;y)=(a+1;a)} per ogni valore possibile a {\displaystyle a} . A seconda del problema, il compito potrebbe essere quello di trovare una soluzione, o qualche soluzione, o tutte le soluzioni. L'insieme di tutte le soluzioni è detto insieme delle soluzioni. È anche possibile che l'obiettivo sia quello di trovare, tra le possibili, la soluzione migliore sotto qualche aspetto. Problemi di questo tipo sono chiamati problemi di ottimizzazione; risolvere un problema di ottimizzazione non è in genere chiamato "risoluzione di un'equazione". Un'affermazione come "un'equazione in x {\displaystyle x} e y {\displaystyle y} ", o "risolvere per x {\displaystyle x} e y {\displaystyle y} ", significa che le incognite sono quelle indicate: in questo caso x {\displaystyle x} e y {\displaystyle y} .

Questo glossario sulle matrici riporta termini utilizzati per il trattamento di queste entità matematiche, che rivestono grande importanza in svariate branche e applicazioni della scienza. Nelle brevi spiegazioni di ogni voce, le matrici sono denotate con una lettera maiuscola (tipo A), e i suoi elementi con la corrispondente minuscola a due pedici (tipo ai,j), di cui il primo indica la riga, e il secondo la colonna dell'elemento stesso. I lemmi sono in ordine alfabetico senza considerare la parola "matrice" o "matrice di" (per es. la voce "Matrice binaria" va ricercata come "Binaria (matrice)".

Enrico Magenes (Milano, 15 aprile 1923 – Pavia, 2 novembre 2010) è stato un matematico italiano.

In matematica, e più precisamente in algebra lineare, una applicazione multilineare è una funzione che generalizza il concetto di applicazione lineare a più variabili. Esempi classici di applicazioni multilineari sono: una applicazione lineare, il determinante e la traccia, un prodotto scalare o una più generale forma bilineare.Le applicazioni multilineari sono anche alla base della definizione di tensore e forma differenziale, e sono quindi molto usate in topologia differenziale nello studio delle varietà differenziabili. Hanno in particolare importanti applicazioni in fisica, specialmente in relatività generale. Sono sinonimi i termini funzione e mappa multilineare.

In matematica, una norma matriciale è la naturale estensione alle matrici del concetto di norma definito per i vettori.

Aldo Finzi (Mantova, 11 marzo 1878 – Roma, 21 novembre 1934) è stato un matematico italiano.

John Wallis (Ashford, 23 novembre 1616 – Oxford, 28 ottobre 1703) è stato un presbitero e matematico inglese. Wallis ha contribuito allo sviluppo del calcolo infinitesimale. Tra il 1643 e il 1689 è stato capo crittografo del Parlamento del Regno Unito e successivamente della corte reale. A lui si attribuisce anche l'introduzione del simbolo ∞ che denota il concetto matematico di infinito.

In matematica, una σ-algebra (pronunciata sigma-algebra) o tribù (termine introdotto dal gruppo Bourbaki) su di un insieme Ω {\displaystyle \Omega } , è una famiglia di sottoinsiemi di Ω {\displaystyle \Omega } che ha delle proprietà di chiusura rispetto ad alcune operazioni insiemistiche, in particolare l'operazione di unione numerabile e di passaggio al complementare. La struttura di σ-algebra è particolarmente utile nelle teorie della misura e probabilità ed è alla base di tutte le nozioni di misurabilità, sia di insiemi che di funzioni. Essa è un caso particolare di algebra di insiemi e, rispetto a quest'ultima, è utilizzata molto più ampiamente in Analisi (per via delle numerose proprietà che le misure definite su σ-algebre hanno rispetto alle operazioni di passaggio al limite). Le σ-algebre che ricorrono più spesso in matematica sono le σ-algebre boreliane e la σ-algebra di Lebesgue. Anche storicamente queste due classi di σ-algebre hanno motivato lo sviluppo del concetto stesso di σ-algebra, nato a cavallo di XIX secolo e XX secolo col fine di formalizzare la teoria della misura. Esso, infatti, precisa l'idea euristica di evento o insieme misurabile. Molte importanti strutture astratte, al centro dei progressi della matematica dell'ultimo secolo, sono definibili mediante σ-algebre.