biblio toscana

La matematica (dal greco μάθημα (máthema), traducibile con i termini "scienza", "conoscenza" o "apprendimento"; μαθηματικός (mathematikós) significa "incline ad apprendere") è la disciplina che studia le quantità (i numeri), lo spazio, le strutture e i calcoli.Per l'origine del termine occorre andare al vocabolo egizio maat, nella cui composizione appare il simbolo del cubito, strumento di misura lineare, un primo accostamento al concetto matematico. Simbolo geometrico di questo ordine è un rettangolo, da cui sorge la testa piumata della dea egizia Maat, personificazione dei concetti di ordine, verità e giustizia. Figlia di Ra, unico Uno, creatore di ogni cosa, la sua potenza demiurgica è limitata e ordinata da leggi naturali e matematiche. All'inizio del papiro di Rhind si trova questa affermazione: "Il calcolo accurato è la porta d'accesso alla conoscenza di tutte le cose e agli oscuri misteri". Il termine maat riappare in copto, in babilonese e in greco. In greco la radice ma, math, met entra nella composizione di vocaboli contenenti le idee di ragione, disciplina, scienza, istruzione, giusta misura, e in latino il termine materia indica ciò che può essere misurato. Col termine matematica di solito si designa la disciplina (e il relativo corpo di conoscenze) che studia problemi concernenti quantità, estensioni e figure spaziali, movimenti di corpi, e tutte le strutture che permettono di trattare questi aspetti in modo generale. La matematica fa largo uso degli strumenti della logica e sviluppa le proprie conoscenze nel quadro di sistemi ipotetico-deduttivi che, a partire da definizioni rigorose e da assiomi riguardanti proprietà degli oggetti definiti (risultati da un procedimento di astrazione, come triangoli, funzioni, vettori ecc.), raggiunge nuove certezze, per mezzo delle dimostrazioni, attorno a proprietà meno intuitive degli oggetti stessi (espresse dai teoremi). La potenza e la generalità dei risultati della matematica le ha reso l'appellativo di regina delle scienze: ogni disciplina scientifica o tecnica, dalla fisica all'ingegneria, dall'economia all'informatica, fa largo uso degli strumenti di analisi, di calcolo e di modellazione offerti dalla matematica.

La storia della matematica ha origine con il concetto di numero e con le prime scoperte matematiche, proseguendo attraverso l'evoluzione nel corso dei secoli dei propri metodi e delle notazioni matematiche il cui uso si sussegue nel tempo. Un aspetto importante della matematica consiste nel fatto che essa si è sviluppata indipendentemente in culture completamente differenti arrivando in molti casi agli stessi risultati: spesso un contatto o una reciproca influenza tra popoli differenti ha portato all'introduzione di nuove idee e a un avanzamento delle conoscenze matematiche, a volte si è visto invece un regredire improvviso della cultura matematica presso alcuni popoli; la matematica moderna ha invece potuto avvalersi dei contributi di persone di tutti i paesi. L'attività svolta dai matematici moderni è molto diversa da quella dei primi matematici delle civiltà antiche; inizialmente la matematica si basò sul concetto di numero, concetto sviluppatosi nella preistoria. La matematica è stata infatti una tra le prime discipline a svilupparsi: evidenze archeologiche mostrano la conoscenza rudimentale di alcune nozioni matematiche molto prima dell'invenzione della scrittura.

Un matematico è una persona che effettua studi, ricerche e sperimentazioni riguardanti problemi della matematica. Alcuni scienziati di altri campi di ricerca possono essere considerati matematici se la loro ricerca offre nuove idee matematiche; un esempio notevole è Edward Witten. Al contrario, alcuni matematici possono studiare problemi matematici relativi ad altri settori della ricerca scientifica e tecnologica (es. fisica matematica), queste persone sono conosciute come matematici applicati.

L'analisi matematica è il ramo della matematica che si occupa delle proprietà che emergono dalla scomposizione infinita di un oggetto denso. Si fonda sul calcolo infinitesimale, con il quale, attraverso le nozioni di limite e continuità, studia il comportamento locale di una funzione utilizzando gli strumenti del calcolo differenziale e del calcolo integrale. Introducendo per il calcolo concetti problematici, quali quello di infinito e di limite, si può passare all'indagine che le ha permesso di divenire basilare in diverse discipline scientifiche e tecniche (dalle scienze naturali all'ingegneria, dall'informatica all'economia), dove viene spesso coniugata con l'analisi numerica.

Fra Luca Bartolomeo de Pacioli, o anche Paciolo (Borgo Sansepolcro, 1445 circa – Roma, 19 giugno 1517), è stato un religioso, matematico ed economista italiano, autore della Summa de Arithmetica, Geometria, Proportioni et Proportionalita e della Divina Proportione. Egli è riconosciuto come il fondatore della ragioneria.

Federigo Enriques (Livorno, 5 gennaio 1871 – Roma, 14 giugno 1946) è stato un matematico, storico della scienza e filosofo italiano.

Questo è un glossario della simbologia matematica costituito da tabelle dedicate ai simboli utilizzati in matematica.

L'analisi numerica (detta anche calcolo numerico o calcolo scientifico) è una branca della matematica applicata che risolve i modelli prodotti dall'analisi matematica alle scomposizioni finite normalmente praticabili, coinvolgendo il concetto di approssimazione. I suoi strumenti, detti algoritmi, sono caratterizzabili in base a velocità di convergenza, stabilità numerica e computabilità.

Gli Elementi (in greco antico: Στοιχεῖα, Stoichêia) di Euclide (matematico greco attivo intorno al 300 a.C.) sono la più importante opera matematica giuntaci dalla cultura greca antica. Contengono una prima formulazione di quella che oggi è conosciuta con il nome di geometria euclidea, rappresentando un quadro completo e definito dei principi della geometria noti al tempo. Oggi questi principi vengono formulati in modo più generale con i metodi dell'algebra lineare. La formulazione fatta da Euclide viene però ancora insegnata nelle scuole secondarie per fornire un primo esempio di sistema assiomatico e di dimostrazione rigorosa. L'opera consiste di 13 libri: i primi sei riguardanti la geometria piana, i successivi quattro i rapporti tra grandezze (in particolare il decimo libro riguarda la teoria degli incommensurabili) e gli ultimi tre la geometria solida. Alcune edizioni più antiche attribuiscono ad Euclide anche due ulteriori libri che la critica moderna assegna però ad altri autori. I diversi libri sono strutturati in definizioni e proposizioni (enunciati che potremmo anche chiamare teoremi). Delle proposizioni vengono fornite le dimostrazioni.

Federico Enriques (Udine, 3 agosto 1941) è un editore e politico italiano.

Archimede di Siracusa (in greco antico: Ἀρχιμήδης, Archimédēs; Siracusa, 287 a.C. circa – Siracusa, 212 a.C.) è stato un matematico, fisico e inventore siceliota. Considerato come uno dei più grandi scienziati e matematici della storia, contribuì ad avanzare la conoscenza in settori che spaziano dalla geometria all'idrostatica, dall'ottica alla meccanica: fu in grado di calcolare la superficie e il volume della sfera e intuì le leggi che regolano il galleggiamento dei corpi; in campo ingegneristico, scoprì e sfruttò i principi di funzionamento delle leve e il suo stesso nome è associato a numerose macchine e dispositivi, come la vite di Archimede, a dimostrazione della sua capacità inventiva; circondate ancora da un alone di mistero sono invece le macchine da guerra che Archimede avrebbe preparato per difendere Siracusa dall'assedio romano. La sua vita è ricordata attraverso numerosi aneddoti, talvolta di origine incerta, che hanno contribuito a costruire la figura dello scienziato nell'immaginario collettivo. È rimasta celebre nei secoli, ad esempio, l'esclamazione èureka! (εὕρηκα! - ho trovato!) a lui attribuita dopo la scoperta del principio sul galleggiamento dei corpi che ancora oggi porta il suo nome.

L'algebra (dall'arabo الجبر, al-ğabr, 'completamento') è una branca della matematica che tratta lo studio di strutture algebriche, relazioni e quantità.

Leonardo di ser Piero da Vinci (Anchiano, 15 aprile 1452 – Amboise, 2 maggio 1519) è stato un inventore, artista e scienziato italiano. Uomo d'ingegno e talento universale del Rinascimento, considerato uno dei più grandi geni dell'umanità, incarnò in pieno lo spirito della sua epoca, portandolo alle maggiori forme di espressione nei più disparati campi dell'arte e della conoscenza: fu infatti scienziato, filosofo, architetto, pittore, scultore, disegnatore, trattatista, scenografo, anatomista, botanico, musicista, ingegnere e progettista.

Giovanni Ricci (Firenze, 17 agosto 1904 – Milano, 9 settembre 1973) è stato un matematico e accademico italiano.

Il V postulato di Euclide è il postulato più conosciuto fra quelli che il matematico Euclide enuncia nei suoi Elementi. I matematici si sono cimentati per più di duemila anni nel tentativo di dedurlo dai primi quattro postulati, finché nell'Ottocento hanno effettivamente dimostrato la sua indeducibilità. Modificando questo postulato si creano geometrie diverse, dette non euclidee.

Il Liber quadratorum di Leonardo Fibonacci è un importante trattato di argomento algebrico in lingua latina. L'opera, che fu pubblicata intorno al 1225, si apre con un'epistola di dedica a Federico II di Hohenstaufen, in cui si afferma che fu il maestro Domenico, già destinatario della Practica geometriae, a presentare il matematico all'imperatore: Nel Liber quadratorum Fibonacci discute la risoluzione di due quesiti: il primo, che gli fu posto dal maestro Giovanni da Palermo, consiste nel calcolare un numero quadrato tale che, aumentato o diminuito di cinque, dia come risultato un numero quadrato; il secondo, che invece gli fu posto dal maestro Teodoro di Antiochia, consiste nel rinvenire tre numeri «tali che la loro somma, aggiunta al quadrato del primo, sia un numero quadrato; che questo numero quadrato, aumentato del quadrato del secondo, sia un numero quadrato e che anche quest’ultimo, sommato al quadrato del terzo, dia un quadrato (equazioni pitagoriche)»

Matematica e architettura sono correlate, poiché, come con altre arti, gli architetti usano la matematica per diverse ragioni. Oltre alla matematica necessaria per la progettazione di edifici, gli architetti usano la geometria per definire la forma spaziale di un edificio, dai Pitagorici del VI secolo a.C. in poi, per creare forme considerate armoniose, e quindi per disporre gli edifici e l'ambiente circostante secondo principi matematici, estetici e talvolta religiosi, per decorare edifici con oggetti matematici come tassellatura e per raggiungere obiettivi ambientali, come ridurre al minimo la velocità del vento attorno alle basi di edifici molto alti. Nell'antico Egitto, nell'antica Grecia, in India e nel mondo islamico, furono costruiti edifici come piramidi, templi, moschee, palazzi e mausolei con proporzioni specifiche per motivi religiosi. Nell'architettura islamica, forme geometriche e motivi geometrici nella piastrellatura sono utilizzati per decorare edifici, sia all'interno che all'esterno. Alcuni templi indù hanno una struttura simile a un frattale in cui le parti assomigliano al tutto, trasmettendo un messaggio sull'infinito nella cosmologia indù. Nell'architettura cinese, i tulou della provincia del Fujian sono strutture difensive circolari e molto comuni. Nel XXI secolo, gli ornamenti matematici vengono nuovamente utilizzati per coprire edifici pubblici. Nell'architettura rinascimentale, la simmetria e la proporzione sono state deliberatamente enfatizzate da architetti come Leon Battista Alberti, Sebastiano Serlio e Andrea Palladio, influenzati dal De architectura di Vitruvio dell'antica Roma e dall'aritmetica dei Pitagorici dell'antica Grecia. Alla fine del XIX secolo, Vladimir Shukhov in Russia e Antoni Gaudí a Barcellona furono i pionieri nell'uso delle strutture iperboloidi. Nella Sagrada Família, Gaudí incorporava anche paraboloidi iperbolici, tassellazioni, archi catenari, catenoidi, elicoidi e superfici rigate. Nel XX secolo, stili come l'architettura moderna e il decostruttivismo hanno esplorato diverse geometrie per ottenere gli effetti desiderati. Superfici minime sono state sfruttate in coperture simili a tende come all'Aeroporto Internazionale di Denver, mentre Richard Buckminster Fuller ha aperto la strada all'uso delle forti strutture a guscio sottile note come cupole geodetiche.

Johann Friedrich Carl Gauss (in tedesco: Gauß ; latinizzato in Carolus Fridericus Gauss; Braunschweig, 30 aprile 1777 – Gottinga, 23 febbraio 1855) è stato un matematico, astronomo e fisico tedesco, che ha dato contributi determinanti in analisi matematica, teoria dei numeri, statistica, calcolo numerico, geometria differenziale, geodesia, geofisica, magnetismo, elettrostatica, astronomia e ottica. Talvolta definito «il Principe dei matematici» (Princeps mathematicorum) come Eulero o «il più grande matematico della modernità» (in opposizione ad Archimede, considerato dallo stesso Gauss come il maggiore fra i matematici dell'antichità), è annoverato fra i più importanti matematici della storia avendo contribuito in modo decisivo all'evoluzione delle scienze matematiche, fisiche e naturali. Definì la matematica come «la regina delle scienze».

Anna Maria Enriques Agnoletti (Bologna, 1907 – Sesto Fiorentino, 12 giugno 1944) è stata una partigiana italiana. Fucilata dai nazisti, è stata insignita di Medaglia d'oro al valor militare alla memoria.

La Fenomenologia dello spirito (in tedesco Phänomenologie des Geistes) è un'opera filosofica di Hegel, pubblicata per la prima volta nel 1807 dove si descrive il percorso che ogni individuo deve compiere, partendo dalla sua coscienza, per identificare le manifestazioni (la "scienza di ciò che appare", la "fenomenologia") attraverso le quali lo spirito si innalza dalle forme più semplici di conoscenza a quelle più generali fino al sapere assoluto.

Il liceo scientifico statale Federigo Enriques di Livorno, dedicato al matematico e filosofo livornese di origine ebraica, è uno dei licei scientifici più antichi d'Italia, essendo stato costituito per mezzo della riforma Gentile del 1923.

L'Italia (/iˈtalja/, ), ufficialmente Repubblica Italiana, è uno Stato situato nell'Europa meridionale, il cui territorio coincide in gran parte con l'omonima regione geografica. L'Italia è una repubblica parlamentare e conta una popolazione di circa 60 milioni di abitanti. La capitale è Roma. La parte continentale, delimitata dall'arco alpino, confina a nord, da ovest a est, con Francia, Svizzera, Austria e Slovenia; il resto del territorio, circondato dai mari Ligure, Tirreno, Ionio e Adriatico, si protende nel mar Mediterraneo, occupando la penisola italiana e numerose isole (le maggiori sono Sicilia e Sardegna), per un totale di 302072,84 km². Gli Stati della Città del Vaticano e di San Marino sono enclavi della Repubblica mentre Campione d'Italia è l'unica exclave italiana. Con l'ascesa di Roma, che fu capitale della Repubblica romana e poi dell'Impero romano, si ebbe il primo processo di unificazione della penisola, destinata a rimanere per secoli il centro politico e culturale della civiltà occidentale. Dopo la caduta dell'Impero romano d'Occidente, l'Italia medievale fu soggetta a invasioni e dominazioni di popolazioni germaniche, come gli Ostrogoti, i Longobardi e i Normanni, perdendo la propria unità politica. Nel XV secolo, con la diffusione del Rinascimento, ridivenne il centro culturale del mondo occidentale, ma dopo le guerre d'Italia del XVI secolo ricadde sotto l'egemonia delle potenze straniere, quali Francia, Spagna e Austria. Durante il Risorgimento gli italiani combatterono per l'indipendenza nazionale e per l'Unità d'Italia, finché nel 1861 fu proclamato il Regno d'Italia, che completò la riunificazione con la presa di Roma del 20 settembre 1870 e la vittoria nella prima guerra mondiale. Dal 1882 al 1960 l'Italia ha posseduto un impero coloniale. Nel 1946, dopo il ventennio fascista, la sconfitta nella seconda guerra mondiale e la guerra civile, a seguito di un referendum istituzionale lo Stato italiano divenne una repubblica. Nel 2020 l'Italia, ottava potenza economica mondiale e terza nell'Unione europea, è un paese con un alto standard di vita: l'indice di sviluppo umano è molto alto, 0.883, e la speranza di vita è di 83,4 anni. È membro fondatore dell'Unione europea, della NATO, del Consiglio d'Europa e dell'OCSE; aderisce all'ONU e al trattato di Schengen. È inoltre membro del G7 e del G20, partecipa al progetto di condivisione nucleare della NATO, è una grande potenza regionale europea, in grado di esercitare influenza politica anche su scelte e decisioni di ordine extra-europeo e globale, e si colloca in nona posizione nel mondo per spesa militare. In virtù della sua storia ultramillenaria, l'Italia vanta insieme alla Cina il maggior numero di siti dichiarati patrimonio dell'umanità dall'UNESCO.

Giovanni Prodi (Scandiano, 28 luglio 1925 – Pisa, 29 gennaio 2010) è stato un matematico italiano, noto anche per le sue molteplici attività riguardanti l'insegnamento della matematica.

La geometria (dal latino geometrĭa e questo dal greco antico "γεωμετρία", composto dal prefisso geo che rimanda alla parola γή = "terra" e μετρία, metria = "misura", tradotto quindi letteralmente come misurazione della terra) è quella parte della scienza matematica che si occupa delle forme nel piano e nello spazio e delle loro mutue relazioni.

Gian Carlo Duranti (Ventimiglia, 13 marzo 1922 – Bussana, 19 marzo 2013) è stato un saggista italiano. Laureatosi in ingegneria edile al Politecnico di Torino ha iniziato nel 1968 ad occuparsi della matematica filosofica greca. Ha pubblicato in proprio un primo libro (Logismi e numeri di Platone) nel 1978. In seguito si è occupato del X libro degli Elementi di Euclide nel quale ritiene di aver rintracciato la matrice egizia della cultura greca, come riportato nel volume Terzo numero binomiale di Euclide e terza civiltà di Ammon-Zeus, pubblicato nel 1991, cui ha fatto seguito nel 1993 Aritmogeometria pitagorica e idee numeri di Platone. In seguito si è occupato della Bibbia ebraica, ritenendo di riportare alla luce una concezione comune al mondo mediterraneo. Tale concezione è stata riportata nelle pubblicazioni Le ‘troisieme Dieu’ d'Abraham et de Platon (1993), Codici nel Pentateuco e matematica egizio platonica (1994), Verso un Platone terzo. Intuizioni e decezioni nella scuola di Tübingen (1995). Sono seguiti nel 2000 Da Giza_Sion_Atene, per una città della scienza, nel 2002 "Dall'antica sapienza mediterranea una sfida agli epigoni dell'Illuminismo", articolo pubblicato in Studi Europei. Nell'anno accademico 2001/2002 l'autore ha tenuto all'Università di Genova un corso monografico di lezioni, intitolato “Filosofia e matematica in Platone e nell'Antico Testamento”, presentato nel volume “Filosofia antica e odierna misosofia” (2002). Nel 2010 ha pubblicato La Bibbia si apre anche al non-credente ,in cui si propone di rispondere all'aspirazione di ogni credente a vedere confermata la Fede dalla ragione. Alla fine del 2012 sono stati pubblicati tre brevi scritti strettamente collegati fra loro: Introduzione al messaggio meta-matematico del Pentateuco; Il compimento dell'Era degli Evi avverrà quando questo Vangelo che annunzia il Regno (dei Cieli) sarà predicato su tutta la Terra abitata, quale testimonianza a tutte le genti (Matteo 24:3-14); La meta-matematica epimoria: scienza peculiare delle Sacre Scritture.

Giovanni Enriques (Bologna, 24 gennaio 1905 – Milano, 21 maggio 1990) è stato un dirigente d'azienda e editore italiano.

Euclide (in greco antico: Εὐκλείδης, Eukléidēs; IV secolo a.C. – III secolo a.C.) è stato un matematico e filosofo greco antico. Si occupò di vari ambiti, dall’ottica all’astronomia, dalla musica alla meccanica, oltre, ovviamente, alla matematica. Gli "Elementi", il suo lavoro più noto, è una delle più influenti opere di tutta la storia della matematica e fu uno dei principali testi per l'insegnamento della geometria dalla sua pubblicazione fino agli inizi del ‘900.

Angiolo Procissi (Prato, 6 dicembre 1908 – Firenze, 28 agosto 1987) è stato un matematico e storico della matematica italiano.

Fortran (o FORTRAN - acronimo di FORmula TRANslation (o TRANslator) ovvero "traduzione (o traduttore) di formule" - è uno dei primi linguaggi di programmazione, sviluppato a partire dal 1954 da un gruppo di lavoro guidato da John Backus; il primo manuale di riferimento per i programmatori in FORTRAN I, The FORTRAN automatic coding system for the IBM 704 EPDM, scritto dallo stesso Backus, è del 1956, mente il compilatore fu pubblicato nel 1957.

Questa è una lista di classici greci conservati, ossia antiche opere letterarie in lingua greca giunte fino a noi, per diverse vie. Comprende sia opere integre sia opere incomplete o lacunose, di cui però si conservi un numero rilevante di parti. Le opere sono ripartite in sezioni secondo un ordine cronologico; all'interno delle singole sezioni sono elencate in ordine alfabetico.

Leonida Tonelli (Gallipoli, 19 aprile 1885 – Pisa, 12 marzo 1946) è stato un matematico italiano, uno dei maggiori analisti della prima metà del XX secolo.

La successione di Fibonacci (detta anche successione aurea), indicata con F n {\displaystyle F_{n}} o con F i b ( n ) {\displaystyle Fib(n)} , in matematica indica una successione di numeri interi in cui ciascun numero è la somma dei due precedenti, eccetto i primi due che sono, per definizione: F 0 = 0 {\displaystyle F_{0}=0} e F 1 = 1 {\displaystyle F_{1}=1} . Questa successione è definita ricorsivamente secondo la seguente regola: F 0 = 0 , {\displaystyle F_{0}=0,} F 1 = 1 , {\displaystyle F_{1}=1,} F n = F n − 1 + F n − 2 {\displaystyle F_{n}=F_{n-1}+F_{n-2}} (per ogni n>1)Gli elementi F n {\displaystyle F_{n}} sono anche detti numeri di Fibonacci. I primi termini della successione di Fibonacci, che prende il nome dal matematico pisano del XIII secolo Leonardo Fibonacci, sono: 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , … {\displaystyle 0,1,1,2,3,5,8,13,21,34,55,89,144,233,\dots }

Benedetto Castelli, al secolo Antonio Castelli (Brescia, 1578 – Roma, 9 aprile 1643), è stato un monaco cristiano, matematico, fisico e accademico italiano.

La geometria euclidea è un sistema matematico attribuito al matematico alessandrino Euclide, che la descrisse nei suoi Elementi. La sua geometria consiste nell'assunzione di cinque semplici e intuitivi concetti, detti assiomi o postulati e, nella derivazione da detti assiomi, di altre proposizioni (teoremi) che non abbiano alcuna contraddizione con essi. Questa organizzazione della geometria permise l'introduzione della retta, del piano, della lunghezza e dell'area. Sebbene molte delle conclusioni di Euclide fossero già conosciute dai matematici, egli mostrò come queste potessero essere organizzate in una maniera deduttiva e con un sistema logico. Gli Elementi di Euclide incominciano con un'analisi della geometria piana, attualmente insegnata nelle scuole secondarie e utilizzata come primo approccio alle dimostrazioni matematiche, per poi passare alla geometria solida in tre dimensioni. Dopo Euclide sono nati particolari tipi di geometrie che non necessariamente rispettano i cinque postulati; tali geometrie sono definite non euclidee.

Questo è un elenco di cimiteri e mausolei di tutto il mondo. I motivi che rendono notevoli questi cimiteri comprendono la loro architettura, la loro storia o le personalità che in essi sono sepolte. I cimiteri costituiscono una preziosa fonte di conoscenza antropologica e spesso rivestono notevole pregio artistico e monumentale, oltre a costituire diretta evidenza dell'esistenza delle persone sepolte, e delle differenze di espressione del culto dei defunti attraverso le culture, le religioni e le forme di stato. Sotto quest'ultimo aspetto, in quanto in molti ordinamenti i cimiteri vengono regolamentati alla stregua di monumenti pubblici con attribuzione di carattere ove più ove meno sacrale, lo stesso aspetto dei cimiteri è anche il frutto della stratificazione delle diverse normazioni cui nel tempo sono stati sottoposti. Le forme recintate, tipiche di alcuni sistemi sociali, sono contrapposte a quelle aperte; le forme monumentali sono contrapposte a quelle semplici (il ricorso a una semplice pietra o al solo simbolo religioso); diversi altri elementi strutturali e simbolici, fra i quali non ultima l'ubicazione urbana o extra muros, sono solo alcuni fra gli aspetti il cui confronto è di diretto rilievo nell'ambito di diverse discipline di studio.

Il Codice Atlantico (Codex Atlanticus) è la più ampia raccolta di disegni e scritti di Leonardo da Vinci. È conservato presso la Biblioteca Ambrosiana di Milano.

Dorothy Johnson Vaughan (Kansas City, 20 settembre 1910 – Hampton, 10 novembre 2008) è stata una matematica e programmatrice statunitense afro-americana che ha lavorato per il National Advisory Committee for Aeronautics (NACA) e successivamente per la NASA, al Langley Research Center a Hampton, in Virginia. Prima di raggiungere il Langley Research Center della NACA nel 1943, Vaughan fu professoressa di matematica alla R. R. Moton High School di Farmville, in Virginia. Nel 1949 fu nominata responsabile ad interim della West Area Computers, un gruppo di lavoro composto esclusivamente da matematiche afro-americane, diventando la prima donna afro-americana a supervisionare un gruppo di dipendenti del centro. Durante i suoi 28 anni di carriera, Vaughan si preparò all'introduzione dei computer all'inizio degli anni '60, insegnando a sé stessa e al suo staff il linguaggio di programmazione Fortran; in seguito diresse la sezione di programmazione della Analysis and Computation Division (ACD) a Langley e partecipò al progetto Scout.La Vaughan è una delle tre donne presenti nel libro del 2016 di Margot Lee Shetterly Il diritto di contare (Hidden Figures in originale). È stato adattato sempre nel 2016 nel film biografico omonimo.

Il Liber abbaci, noto anche come Liber abaci, è un trattato di argomento matematico. Scritto in latino medievale nel 1202 dal matematico pisano Leonardo Fibonacci, che nel 1228 ne pubblicò una seconda stesura, ha svolto un ruolo fondamentale nella storia della matematica occidentale ed è ritenuto uno dei libri più importanti e fecondi del Medioevo.Il Liber abbaci è un ponderoso trattato di aritmetica e algebra con il quale, all'inizio del XIII secolo, Fibonacci ha introdotto in Europa il sistema numerico decimale indo-arabico e i principali metodi di calcolo ad esso relativi. Il libro non tratta l'utilizzo dell'abaco, sicché il suo titolo può essere tradotto in Libro del calcolo: dato che abaco per i greci, i romani e i maestri d'abaco dei secoli precedenti era uno strumento di calcolo, secondo alcuni studiosi il titolo non sarebbe autoriale, per quanto non vi siano dubbi che il Fibonacci abbia in effetti riservato questa denominazione all'aritmetica-algebra applicativa in genere. Su questo trattato, per oltre tre secoli, si formeranno maestri e allievi della scuola toscana. L'equilibrio fra teoria e pratica era di fatto raggiunto. Fibonacci dice: "Ho dimostrato con prove certe quasi tutto quello che ho trattato". Quando Fibonacci scrisse il trattato, in Europa gli scritti di matematica avanzata erano quasi del tutto inesistenti, a parte le traduzioni delle opere classiche (gli Elementi di Euclide, per esempio), che però erano ancora molto poco diffuse, e i cosiddetti Algorismi, scritti di aritmetica latina che prendevano il nome dal matematico al-Khwarizmi. Fibonacci compì un'operazione unica, diversa da quelle degli Arabi, se non per l'originalità certo per la mole. La prima edizione a stampa del Liber abbaci è stata curata da Baldassarre Boncompagni Ludovisi nel 1857, che si basò su un manoscritto di XIV secolo recante al suo interno una versione databile al 1228.

Emma Castelnuovo (Roma, 12 dicembre 1913 – Roma, 13 aprile 2014) è stata un'insegnante e matematica italiana, figlia del matematico Guido Castelnuovo. Ha dato significativi contributi alla didattica della matematica, rivoluzionando completamente il modo di insegnare la materia (e in modo particolare la geometria euclidea). Ha collaborato a lungo con Bruno de Finetti.

La filosofia della matematica è la branca della filosofia della scienza che cerca di dare risposta a domande quali: "perché la matematica è utile nella descrizione della natura?", "in quale senso, qualora se ne trovi uno, le entità matematiche (in particolare i numeri) esistono?" "perché e in che modo gli enunciati matematici sono veri?". In questo articolo sono presentati i vari approcci che vengono seguiti per rispondere a questioni come le precedenti. È utile precisare che tre sono i problemi della filosofia della matematica: Un problema ontologico: risponde alla domanda "Esistono i numeri?"; Un problema metafisico: risponde alla domanda "Che cosa sono i numeri?"; Un problema epistemologico: "Come facciamo ad accedere epistemicamente alle verità della matematica o, meglio, come possiamo sapere che ciò che ci dice la matematica è vero?";Questi sono i problemi che la maggior parte dei filosofi, oggigiorno, ritengano debbano essere risolti da una buona filosofia della matematica.

L'Albero di Fibonacci è un albero AVL che, data una determinata altezza, ha il minor numero possibile di nodi mantenendo il bilanciamento. Questo particolare tipo di albero prende il nome dall'omonimo matematico Leonardo Fibonacci. L'albero ha infatti le caratteristiche della famosa successione, è infatti intrinsecamente ricorsivo. Lo si evince dal fatto che qualsiasi albero di Fibonacci di altezza h può essere costruito a partire da una radice e da un sottoalbero di altezza h-2 come sottoalbero destro e h-1 come sottoalbero sinistro. Si verifica intuitivamente e visivamente che il coefficiente di bilanciamento di ogni singolo nodo dell'albero è +1. Quindi questa categoria di alberi è quella che più si avvicina alla condizione di sbilanciamento, pur essendo ovviamente ancora bilanciato.

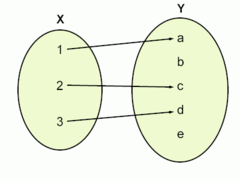
In matematica, una funzione è una relazione tra due insiemi, chiamati dominio e codominio della funzione, che associa a ogni elemento del dominio uno e un solo elemento del codominio. Se i due insiemi sono rispettivamente indicati con X {\displaystyle X} e Y {\displaystyle Y} , la relazione è indicata con f : X → Y {\displaystyle f\colon X\to Y} e l’elemento associato a x ∈ X {\displaystyle x\in X} tramite la funzione f {\displaystyle f} viene abitualmente indicato con f ( x ) {\displaystyle f(x)} (si pronuncia “effe di x”).

La storia della matematica è stata sempre costellata dalla questione dei problemi irrisolti, vale a dire quelle congetture e domande delle quali non solo non si conosce la risposta, ma che sembrano sfide inattaccabili con i mezzi dell'indagine matematica dell'epoca in cui sono proposte. La loro soluzione, avvenuta a volte a distanza di secoli, si è spesso dimostrata in grado di schiudere nuovi orizzonti allo sviluppo del pensiero matematico, richiedendo, a volte, l'inquadramento del problema in un contesto matematico diverso da quello della formulazione originaria.

Leonardo Pisano detto il Fibonacci (Pisa, settembre 1170 circa – Pisa, 1242 circa) è stato un matematico italiano. È considerato uno dei più grandi matematici di tutti i tempi. Con altri dell'epoca contribuì alla rinascita delle scienze esatte dopo la decadenza dell'età tardo-antica e dell'Alto Medioevo. Con lui, in Europa, ci fu l'unione fra i procedimenti della geometria greca euclidea (gli Elementi) e gli strumenti matematici di calcolo elaborati dalla scienza araba (in particolare egli studiò per la parte algebrica il Liber embadorum dello studioso ebreo spagnolo Abraham ibn ‛Ezra).

L'Adorazione dei Magi è un dipinto a olio su tavola e tempera grassa (246×243 cm) di Leonardo da Vinci, realizzato tra il 1481 e il 1482. Viene conservato nella Galleria degli Uffizi a Firenze.

Cesarina Tibiletti (Milano, 17 novembre 1920 – Milano, 7 novembre 2005) è stata una matematica e accademica italiana.

I codici di Leonardo da Vinci sono raccolte di annotazioni, appunti e disegni realizzati da Leonardo da Vinci nel corso della propria vita su argomenti diversi.

Il Divina Proportione è il trattato di Fra' Luca Pacioli sulle applicazioni della sezione aurea.